
We use MathJax
The standard method of depreciation for federal income tax purposes is called the Modified Accelerated Cost Recovery System, or MACRS. Essentially, a MACRS depreciation schedule will begin with a declining balance method, then switch to a straight line schedule to finish the schedule. The MACRS method was introduced in 1986, and generally property placed into service after that date will be depreciated according to the MACRS method. It is a modification of the Accelerated Cost Recovery System, or ACRS, which was in use from 1981 to 1986. We shall look at the underlying principles of this approach first, then deal with its actual use.
One of the goals of the MACRS method is to remove uncertainties in the current depreciation process, particularly with regard to scrap values and asset lifetimes. The MACRS method assigns each asset a zero scrap value. (If an asset should later be sold, then the sale counts as income.) The method also groups different types of assets into different classes, and assigns each class a specific lifetime. As of 2005, the classes are:
| Life | Asset Types |
| 3-year | Some tractors, horses |
| 5-year | Most road vehicles, computers, office equipment |
| 7-year | Office furniture, farm machinery |
| 10-year | Boats |
| 15-year | Roads, fences |
| 20-year | Farm buildings |
| 27.5-year | Residential real estate |
| 39-year | Nonresidential real estate |
A second goal of the MACRS method is to produce accelerated depreciation. Declining balance methods provide the accelerated depreciation, but they will never produce a zero scrap value without an adjustment of some sort. The MACRS method adjusts the declining balance method by switching to a straight line computation at the point which gives the quickest depreciation of an asset.
In order to understand how the quickest depreciation can be obtained through a combination of declining-balance and straight-line methods, we offer the following example. However, it is not a true MACRS example, because of partial year considerations that would still need to be taken into account.
Example. Fister and Bullhead, a law firm, purchases $12,000 worth of office furniture. They will depreciate the entire cost over the next seven years. Prepare a double declining balance depreciation schedule, switching to straight line at the most opportune time.
Solution. The depreciation rate for the declining balance portion of the schedule is:
$$\text{Annual Depreciation Rate} = \dfrac{200\%}{7} = 28.5714\%$$
The straight line amount depends on the year in which the switch between methods will be made, and we do not yet know when that will occur. Therefore, we compute a straight line depreciation amount each year by dividing the previous book value by the number of years remaining in the schedule. The declining balance depreciation is computed in the usual fashion. We use the larger of the two amounts as the current depreciation. The schedule is:
| Year | Declining Balance Depreciation | Straight Line Depreciation | Current Depreciation | Accumulated Depreciation | Book Value |
| 0 | $\$12,000$ | ||||
| 1 | $12000 \times 0.285714 \approx 3429$ | $\dfrac{12000}{7} \approx 1714$ | $\$3,429$ | $\$3,429$ | $\$8,571$ |
| 2 | $8571 \times 0.285714 \approx 2449$ | $\dfrac{8571}{6} \approx 1429$ | $\$2,429$ | $\$5,878$ | $\$6,122$ |
| 3 | $6122 \times 0.285714 \approx 1749$ | $\dfrac{6122}{5} \approx 1224$ | $\$1,749$ | $\$7,627$ | $\$4,373$ |
| 4 | $4373 \times 0.285714 \approx 1249$ | $\dfrac{4373}{4} \approx 1093$ | $\$1,249$ | $\$8,876$ | $\$3,124$ |
| 5 | $3124 \times 0.285714 \approx 893$ | $\dfrac{3124}{3} \approx 1041$ | $\$1,041$ | $\$9,917$ | $\$2,083$ |
| 6 | $2083 \times 0.285714 \approx 595$ | $\dfrac{2083}{2} \approx 1042$ | $\$1,042$ | $\$10,959$ | $\$1,041$ |
| 7 | $1041 \times 0.285714 \approx 297$ | $\dfrac{1041}{1} = 1041$ | $\$1,041$ | $\$12,000$ | $\$0$ |
Once a switch from declining balance to straight line is made, no further computations for the depreciation amount are necessary. Since the straight line method's basic characteristic is that equal amounts of depreciation will occur each year, once we know the amount, it does not need to be recalculated each time. Notice that in the previous example, we first used the straight line depreciation amount in year 5. The depreciation amounts in years 6 and 7 were identical (except for rounding).
The MACRS method must also be adjusted for partial years of service. Rather than using the standard convention, MACRS adjusts for partial years using the IRS conventions, half-year, mid-quarter, or mid-month. These conventions are built into the tables which the IRS provides for computing depreciation. One of these tables is pictured below. The percents given in the table are based on the original cost of the asset (not on its book value).
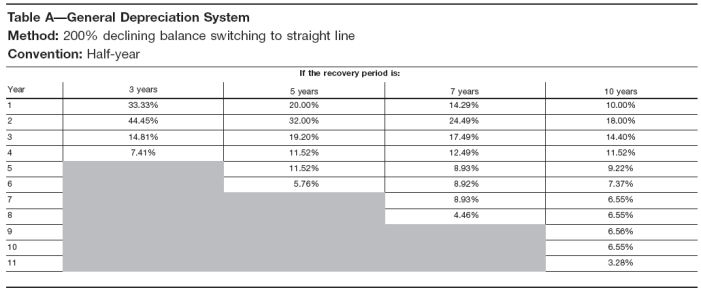
The values in this table are not arbitrary. You should observe that the first year percentage (more noticeably in the 10 year class) is approximately half of the second year percentage. This is a result of the IRS half-year convention being used to adjust for the partial year. The same is true for the last year percentage, when compared with the immediately previous year.
The first year percentage is actually determined from the declining balance depreciation rate formula. Since the 200% Declining Balance Method is used, we can divide 200% by the life in years to obtain the annual depreciation rate. The first year's rate is exactly half of that rate.
We can also observe the transition from declining balance to straight line in most of the classes. In the 7-year class, that transition occurs in year 5, just as we had determined in Example 1.
Tables for the longer classes are similar, but with slightly different assumptions. The 15-year and 20-year classes use the 150% declining balance method and the half-year convention. The 27.5-year and 39-year classes use the straight line method and the mid-month convention. And there are some special cases which result in the use of the 125% declining balance method or the mid-quarter convention.
Example. Parkside School buys 60 graphing calculators at a total cost of $4,800. Prepare a MACRS depreciation schedule.
Solution. Graphing calculators, like computers or office equipment, belong in the 5-year class. To complete the deprecation schedule, we simply multiply the original cost by the rate given in the MACRS depreciation rate table. The result is:
| Year | Current Depreciation | Accumulated Depreciation | Book Value |
| 0 | $\$4,800$ | ||
| 1 | $4800 \times 0.20 = 960$ | $\$960$ | $\$3,840$ |
| 2 | $4800 \times 0.32 = 1536$ | $\$2,496$ | $\$2,304$ |
| 3 | $4800 \times 0.1920 \approx 922$ | $\$3,418$ | $\$1,382$ |
| 4 | $4800 \times 0.1152 \approx 553$ | $\$3,971$ | $\$829$ |
| 5 | $4800 \times 0.1152 \approx 553$ | $\$4,524$ | $\$276$ |
| 6 | $4800 \times 0.0576 \approx 276$ | $\$4,800$ | $\$0$ |