The Intermediate Value Theorem

We already know from the definition of continuity at a point that the graph of a function will not have a hole at any point where it is continuous. The Intermediate Value Theorem basically says that the graph of a continuous function on a closed interval will have no holes on that interval.

Statement of the Theorem

Suppose $f(x)$ is continuous on the closed interval $[a,b]$. If $L$ is a real number between the values $f(a)$ and $f(b)$, but not equal to either of them, then there exists a number $c$ in the interval $[a,b]$. for which $f(c)=L$.

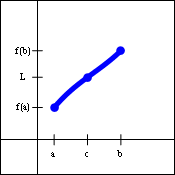
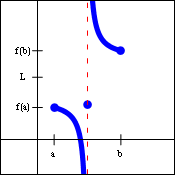
The graph on the left below illustrates the situation described by the theorem. Since the function $f(x)$ is continuous, the endpoints of the interval are connected by the graph, and the function will pass through all values between $f(a)$ and $f(b)$. The graph on the right below shows a function that is defined everywhere on the closed interval $[a,b]$, but is not continuous on that interval. The lack of continuity allows for values between $f(a)$ and $f(b)$ that the function never takes on.

Graph of a continuous function on a closed interval

Graph of a non-continuous function on a closed interval

Using the Intermediate Value Theorem

Show that the function $f(x)=x^{17}-3x^4+14$ is equal to 13 somewhere on the closed interval $[0,1]$.

We note that $f(0)=14$ and $f(1)=12$,	By substituting the endpoints of the closed interval into the function, we obtain the values $f(a)$ and $f(b)$.
and $12 < 13 < 14$.	And we note that the value of $L$, 13, does fall between $f(a)$ and $f(b)$.
But $f(x)$ is a polynomial and is therefore continuous everywhere, so in particular it is continuous on the closed interval $[0,1]$.	The continuity of the function is the crux of the issue. Without it, the result could not be guaranteed. So we must demonstrate the continuity of the function on the given interval. And since the function is a polynomial, continuity is automatic.
Therefore, by the Intermediate Value Theorem, there exists a number $c$ in the interval $[0,1]$ for which $f(c)=13$.	Having verified all of the hypotheses of the Intermediate Value Theorem, the conclusion must then follow.

Proof of the Theorem

Even though the statement of the Intermediate Value Theorem seems quite obvious, its proof is actually quite involved, and we have broken it down into several pieces. First, we will discuss the Completeness Axiom, upon which the theorem is based. Then we shall prove Bolzano's Theorem, which is a similar result for a somewhat simpler situation. Then the Intermediate Value Theorem will follow almost immediately.

The Completeness Axiom

Axioms are statements in a mathematical system that are assumed to be true without proof. The Completeness Axiom is an axiom about the real numbers, and is sometimes phrased in the language of least upper bounds. A real number $x$ is called a least upper bound for a set $S$ if the following two properties are true:

The number $x$ is an upper bound for the set $S$. (In other words, if $s$ is any number in set $S$, then $s\le x$.)
If $y

Note that it is not necessary for an upper bound to be in the set $S$. Both upper bounds and least upper bounds could be numbers outside of set $S$.

The statement of the Completeness Axiom is:

If $S$ is a nonempty set of real numbers that is bounded above, then there exists exactly one real number that is the least upper bound of $S$.

To understand this, we shall consider a few examples.

If set $S$ is the closed interval $[3,5]$, then the number 5 is the least upper bound. The value 5 is certainly an upper bound, since for every $s$ in the interval, $s\le 5$. And for any number $y<5$, there is a larger number that is still in the set $S$, namely 5 itself, so $y$ is not an upper bound. The Completeness Axiom states that 5 is the only least upper bound of this interval.
If set $S$ is the open interval $(4,9)$, then the number 9 is the least upper bound. The value 9 is certainly an upper bound, since for every $s$ in the interval, $s\le 9$ (and in fact, $s$ is never equal to 9). And for any number $y<9$, there is a larger number that is still in the set $S$, namely $\dfrac{y+9}{2}$, so $y$ is not an upper bound. The Completeness Axiom states that 9 is the only least upper bound of this interval.
If set $S$ is the interval $(6,\infty)$, then the hypothesis of the Completeness Axiom is not satisfied. In other words, set $S$ is not bounded above, because the values of $S$ continue on to infinity. Therefore, the conclusion of the Completeness Axiom is not guaranteed to follow. And in fact, in this case, the conclusion is not true, since there is no real number that is the least upper bound of this set.
If set $S$ consists of the numbers of the sequence $a_n=\left\{\left. 7-\dfrac{1}{n} \right| n \text{ is a positive integer}\right\}$, then the number 7 is the least upper bound. The value 7 is certainly is an upper bound, since $7-\dfrac{1}{n}\le 7$ for all positive integers. And for any number $y<7$, by the Archimedean Property of the real numbers which basically states that there is always a larger value, we can find a positive integer $n$ for which $n>\dfrac{1}{7-y}$. This inequality, when solved for $y$, yields $y<7-\dfrac{1}{n}$, so $y$ is not an upper bound. Thus, the Completeness Axiom states that 7 is the only least upper bound for this set.

Bolzano's Theorem

The statement of Bolzano's Theorem is:

Suppose $f(x)$ is continuous on the closed interval $[a,b]$, and suppose that $f(a)$ and $f(b)$ have opposite signs. Then there exists a number $c$ in the interval $[a,b]$, for which $f(c)=0$.

Proof.

Since $f(a)$ and $f(b)$ have opposite signs, then one is positive and one is negative. Let us first suppose that $f(a)<0$ and $f(b)>0$.	The supposition of opposite signs also implies that neither value is zero itself. That leaves two cases, and we begin with one of them here. The other case will be dealt with later.
Define the set $S=\{x\in [a,b]\|f(x)\le 0\}$.	This set contains all of the values of the function $f(x)$ on the closed interval $[a,b]$ for which the value of $f(x)$ is not positive.
The set $S$ is not empty, since $f(a)<0$, so the number $a$ is in the set. And the set $S$ is bounded above, since $x\le b$ for all values of $x$ in the interval $[a,b]$, and $S$ is a subset of that interval.	Here we are establishing that our set $S$ meets the hypotheses for the Completeness Axiom.
Therefore, $S$ has a least upper bound. Define the value $c$ to be the least upper bound of $S$.	Then we use the Completeness Axiom to establish the existence of the least upper bound, and we give it the name $c$.
Since $f(x)$ is continuous, then $\lim\limits_{x\to c}f(x)=f(c)$.	This is from the definition of continuity, which also states that each of those quantities is a real number.
Now, there are only three possibilities, either $f(c)>0$, or $f(c)<0$, or $f(c)=0$.	This is sometimes referred to as the Trichotomy Property of the real numbers.
So suppose $f(c)>0$. Let $\epsilon_1=\dfrac{f(c)}{2}$. Then $\epsilon_1>0$.	Beginning with the first of the three possibilities for $f(c)$, we define a positive epsilon.
Then there exists a $\delta_1>0$ such that for all $x$, the expression $0 < \|x-c\| < \delta_1$ implies $\|f(x)-f(c)\| < \dfrac{f(c)}{2}$.	This is the definition of the limit applied to the statement $\lim\limits_{x\to c}f(x)=f(c)$, using $\epsilon_1$.
Then $-\dfrac{f(c)}{2} < f(x)-f(c) < \dfrac{f(c)}{2}$, which implies $\dfrac{f(c)}{2} < f(x) < \dfrac{3f(c)}{2}$, and therefore $f(x)$ is positive everywhere in the interval $c-\delta_1 < x < c+\delta_1$.	We expanded the inequality above, then added $f(c)$ to each expression. But since $\epsilon_1$ was positive, this inequality implies $f(x)$ is always positive whenever $0 < \|x-c\| < \delta_1$. The last inequality was obtained by expanding this absolute value inequality involving $\delta_1$.
But $c$ was the least upper bound of the set $S$ which produced non-positive values of $f(x)$, yet it would appear that we found a smaller upper bound, $c-\delta_1$. This is impossible, and therefore $f(c)>0$ is impossible.	Having arrived at a contradiction, we are forced to reject our most recent supposition.
So suppose $f(c)<0$. Let $\epsilon_2=\dfrac{-f(c)}{2}$. A similar argument will show that $f(x)$ is negative everywhere in the interval $c-\delta_2 < x < c+\delta_2$.	So we move onto the second possibility for $f(c)$, define $\epsilon_2$ and $\delta_2$ similarly, and obtain a similar result.
But $c$ was the least upper bound of the set $S$ which produced non-positive values of $f(x)$, yet it would appear that we found a larger value, $c+\delta_2$, in set $S$. This is impossible, and therefore $f(c)<0$ is impossible.	And we obtain a similar contradiction.
Therefore, $f(c)=0$. This proves the first case.	Of the three possibilities for $f(c)$, this is the only possibility remaining. But this was with the assumption that $f(a)<0$ and $f(b)>0$.
For the second case, suppose that $f(a)>0$ and $f(b)<0$. Define $g(x)=-f(x)$, and note that $g(x)$ is continuous on $[a,b]$, $g(a)<0$, and $g(b)>0$.	The continuity and the values of the function $g(x)$ follow immediately from the continuity and values of $f(x)$.
Therefore, by the first (already proven) case, there exists a number $c$ in the interval $[a,b]$ for which $g(c)=0$.	Rather than repeat the entire explanation with the signs of $f(a)$ and $f(b)$ reversed, we use the fact that $g(x)$ meets the conditions already proven in the first case of this theorem, so the result follows for $g(x)$.
Therefore, $f(c)=-g(c)=0$. This proves the second of the two cases, hence the theorem is proven.	And then the result for $f(x)$ is immediately available.

Proof of the Intermediate Value Theorem

Having established Bolzano's Theorem, the Intermediate Value Theorem is a fairly straightforward corollary. First, we shall restate the theorem.

Suppose $f(x)$ is continuous on the closed interval $[a,b]$. If $L$ is a real number between the values $f(a)$ and $f(b)$, but not equal to either of them, then there exists a number $c$ in the interval $[a,b]$. for which $f(c)=L$.

Proof.

Define $g(x)=f(x)-L$. Then the function $g(x)$ is continuous on the closed interval $[a,b]$,	The continuity of $g(x)$ is assured by the Difference Limit Law.
and $g(a)$ and $g(b)$ will have opposite signs.	Here, we needed to know that $L$ was not equal to either $f(a)$ or $f(b)$, so that neither $g(a)$ nor $g(b)$ would be zero.
Then, by Bolzano's Theorem, there exists a number $c$ in the interval $[a,b]$ for which $g(c)=0$.	Since $g(x)$ has met all of the hypotheses of Bolzano's Theorem, the conclusion follows.
Thus, $f(c)-L=0$, and therefore $f(c)=L$.	This results from the definition of $g(x)$.