The Limit Concept and its Definition

Underlying all of calculus is the idea of a limit. In this section, we will explore what a limit is.

Functions with Holes

Through most of your earlier work in mathematics, you worked with some very nice functions. But there are quite a few functions which exhibit some rather unusual behaviors. Consider, for example, the function $f(x)=\dfrac{x^2-4}{x-2}$. Since the denominator cannot equal zero, the domain of this function is $x\ne 2$. Here is the graph of the function.

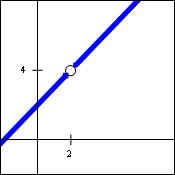
the graph of a line, but with a hole at the point 2 comma 4

So how do we describe the location of the hole? If we don't need to refer to the function itself, we can simply say it is located at $(2,4)$ But if we want to refer to the hole as it relates to this function, things are somewhat more problematic. Note that $f(2)\ne 4$, because $f(2)$ does not exist, so a simple functional value is not available. Since the hole keeps us from referring to the point itself, we could say that the points near the hole have coordinates near the coordinates of the hole. In other words, the behavior of the function near the hole is important.

Closing in on the Hole

Let us suppose now that we have a generic function $y=f(x)$ with a generic point $(x,f(x))$, and with a hole located at the point $(c,L)$. Its graph is given below.

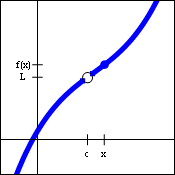
Graph of a function having a hole at the point c comma L, with another nearby point of the function at x comma f of x

To describe the behavior of the function near the hole, we will speak in terms of the point as it approaches the hole. We would like to say:

When the value of $x$ approaches $c$, then the value of $f(x)$ approaches $L$.

That statement roughly describes what is happening, and our notation for this statement, $\lim\limits_{x\to c} f(x)=L$, reflects these very words. The symbol $\lim$ is an abbreviation for the word limit, which is the mathematical term for the concept we are now developing. But the statement doesn't give us much help in turning the situation into something that can be evaluated mathematically. Here is a similar statement:

When the value of $x$ is close to $c$, then the value of $f(x)$ is close to $L$.

This may appear almost identical, but the word "close" does suggest a way to measure (using numbers) what is happening. So here is another statement:

When the distance between $x$ and $c$ is small, then the distance between $f(x)$ and $L$ is small.

Distance is something that is well defined in mathematics. For our situation, we are talking about distances along each axis, and a two-dimensional distance can be found by using absolute values. So we can now write:

When $|x-c|$ is small, then $|f(x)-L|$ is small.

So how do we describe small? It would appear that we have simply moved our original difficulty of a function being "close" to a hole to a new realm, where the distance is "close" to zero. But now, we can define a couple of values (delta and epsilon) that will help force the distances to remain near zero.

When $|x-c|<\delta$, then $|f(x)-L|<\epsilon$.

In fact, we are saying that our distances ought to be less than these values. Both $\delta$ and $\epsilon$ will need to be positive, because our distances are less than those values, and distances cannot be negative. Often, $\delta$ and $\epsilon$ are referred to as infinitesimals, because they are intended to represent very small quantities. In some sense, they can be thought of as tolerances, although as we consider them now, they have nothing to do with error, only closeness. And how do we interpret these values on the graph? Let us update our picture.

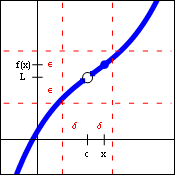
Graph of a function having a hole at the point c comma L, with another nearby point of the function at x comma f of x. Two vertical dashed red lines are located a distance delta from c, and two horizontal dashed red lines are located a distance epsilon from L. The nearby point is within both sets of dashed lines.

In this picture, $\delta$ is the distance along the $x$-axis from the value $c$ to either of the vertical dashed lines. In other words, the vertical dashed lines are located at $c-\delta$ and at $c+\delta$. Since $x$ is between those vertical dashed lines, the statement $|x-c|<\delta$ is being displayed.

Similarly, $\epsilon$ is the distance along the $y$-axis from the value of $L$ to either of the horizontal dashed lines. In other words, the horizontal dashed lines are located at $L-\epsilon$ and at $L+\epsilon$. Since $f(x)$ is between those horizontal dashed lines, the statement $|f(x)-L|<\epsilon$ is also being displayed.

These dashed lines also create a rectangle. Notice that the function exits the rectangle by crossing the left and right sides of the rectangle, and not the top or bottom of the rectangle. This was quite intentional. If we allowed the function to leave the top or bottom of the rectangle, we could conceivably have a much larger gap between the two halves of the function than just a hole we have now. To maintain this relationship between the function and the rectangle, two things are required.

It will not enough that both $|x-c|<\delta$ and $|f(x)-L|<\epsilon$ are true. Instead, we need that $|f(x)-L|<\epsilon$ is true whenever $|x-c|<\delta$ is true. But upon closer examination, we see that $|x-c|<\delta$ is not true at the hole itself, so we need to exclude the hole from consideration. To do this, we modify the inequality to read $0<|x-c|<\delta$. Our required statement must then state that $|f(x)-L|<\epsilon$ is true whenever $0<|x-c|<\delta$ is true. Or alternatively, that $0<|x-c|<\delta$ always implies $|f(x)-L|<\epsilon$.
The implication in the previously bullet can't be true just sometimes. It must be true all the time, so that we avoid situations where a larger gap might occur. To avoid those larger gaps, we need the statements to be true for every possible positive epsilon. Furthermore, that for every possible epsilon (that is, for every $\epsilon >0$), we can draw such a rectangle, and since the rectangle has some length, there must exist a $\delta >0$ such that the implication in the previous bullet holds.

The Definition of the Limit

So here is our definition.

The expression $\lim\limits_{x\to c} f(x)=L$ means: For every $\epsilon >0$, there exists a $\delta >0$, such that for every $x$, the expression $0<|x-c|<\delta$ will imply $|f(x)-L|<\epsilon$.

Example

So how do the concept and the definition relate to our original example of the function $f(x)=\dfrac{x^2-4}{x-2}$? Conceptually, we would say that $\lim\limits_{x\to 2} f(x)=4$, because as the $x$-values approach 2, the function itself approaches the "hole" in the graph, and the $y$-values will be approaching 4. In fact, although the hole is there, the concept allows us to avoid dealing with it entirely.

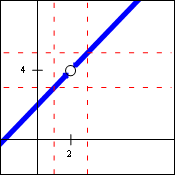
The graph of a line, but with a hole at the point 2 comma 4. Two vertical dashed red lines are located a small distance from c, and two horizontal dashed red lines are located a small distance from 4.

As we compare the definition to the graph, we see five parts:

The phrase "For every $\epsilon >0$ " implies that we can make our horizontal dashed lines as close as we want to the $y$-value 4, as long as we don't let them be equal to 4 itself. In our graph, we have placed those horizontal lines at the $y$-values of 3 and 5 (which means we chose an epsilon value of 1), but it is important to notice that the dashed lines can be moved closer (and epsilon made smaller) without harming the argument.
The phrase "there exists a $\delta >0$ " says that there are vertical dashed lines that will probably be close to the $x$-value 2, but definitely not equal to 2 itself. But this is not the only restriction placed on those vertical lines. We have placed our vertical dashed lines at the $x$-values of 1 and 3 (which means that we are exhibiting a delta value of 1), which is as far as the dashed lines can be apart in this example for the epsilon we originally chose.
The phrase "such that for every $x$" implies simply that no exceptions can be allowed for particular values of $x$.
The phrase "the expression $0<|x-c|<\delta$ " specifies exactly which $x$-values are being used to help define the restrictions on the vertical lines, since this inequality is true for every $x$-value between the vertical lines, except for the value 2 itself. For this example, in other words, for every $x$-value between 1 and 3, not including 2.
The phrase "will imply $|f(x)-L|<\epsilon$ " means that for every point on the function between the vertical lines, the function will also be between the horizontal lines. In this example, in other words, the values of $f(x)$ will have to be between 3 and 5. But remember, this argument must be valid for every epsilon, not just for a single example.