
We use MathJax
There are several ways in which mathematicians will define the number $e$. Whichever approach one takes, it is then necessary to show that the other approaches will arise as a natural consequence of the chosen approach.
Most likely, you first encountered the number $e$ in a discussion on compound interest in a college algebra course. The typical thread of that discussion goes something like this:
The formula $A=P\left(1+\dfrac{r}{n}\right)^{nt}$ gives the balance $A$, after a principal $P$ is deposited at an interest rate $r$ (where $r$ is the decimal form of the percent) for $t$ years, with compounding occurring $n$ times per year. If, for example, we deposited $1,000 for 5 years at 6% interest per year, and compared the various compounding frequencies, we would obtain the following balances.
| Compounding Frequency | Number of Compoundings per Year (n) | Balance (A) |
| annually | 1 | $1,338.23 |
| quarterly | 4 | $1,346.86 |
| monthly | 12 | $1,348.85 |
| daily | 365 | $1,349.83 |
| hourly | 8760 | $1,349.86 |
It would appear that more frequent compoundings do not significantly alter the final balance. So if we continued this argument ad infinitum, and compounded every minute, or every second, or every nanosecond, we ought to reach some sort of limit (compounding every instant). This limit is called continuous compounding.
To isolate the factor in the formula that is causing this type of behavior, we shall define $n=mr$, and substitute this into the formula. We get $A=P\left(1+\dfrac{r}{mr}\right)^{mrt}=P\left[\left(1+\dfrac{1}{m}\right)^m\right]^{rt}$. When $n$ increases without bound (that is, when it is approaching infinity), then $m$ will also increase without bound. Therefore, we need to examine the behavior of the quantity $\left(1+\dfrac{1}{m}\right)^m$ as $m$ approaches infinity. We can do this either numerically, or by using a graph of the function $f(x)=\left(1+\dfrac{1}{x}\right)^x$.
|
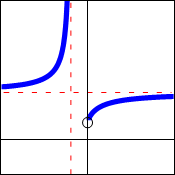 |
With either approach, we see that the values of $\left(1+\dfrac{1}{m}\right)^m$ appear to be approaching the value 2.71828, and this number is called $e$. A more careful analysis would show that $e\approx 2.7182818284590\ldots$. Replacing $\left(1+\dfrac{1}{m}\right)^m$ by $e$ in the compound interest formula, we obtain a formula for continuously compounded interest: $A=Pe^{rt}$.
The college algebra discussion does point out that $e$ is somehow related to a limit, but it essentially swept under the rug a rather important issue. How do we know that the graph really has a horizontal asymptote? How do we know that values don't continually increase beyond 2.71829, or beyond 3, or beyond some other even larger number, if we just choose an $m$ large enough? A more careful exposition follows.
This inequality is an important component of the justification that the limit definition of $e$ actually exists. The two statements below give two forms of the inequality.
The proof requires mathematical induction (which usually appears in a college algebra book, but is often not included in a college algebra course).
Proof
| For $n=0$, we have $(1+a)^0=1=1+0a$. For $n=1$, we have $(1+a)^1=1+a=1+1a$. |
These are the two cases of $n$ which appear in the second statement, but not in the first. |
| For $n=2$, we have $(1+a)^2=1+2a+a^2>1+2a$. | The first stage of a mathematical induction proof requires that we verify the statement for a smallest value of $n$. For the first statement, the smallest value was 2. The inequality holds here because $a\ne 0$, and therefore $a^2$ is a positive number. |
| Now we assume that the inequality is true for $n$, and prove that this implies the inequality for $n+1$ will also be true. | The second stage of a mathematical induction proof requires that we prove a domino effect, in that the formula for a previous integer will always imply the formula for the next integer. That way, the formula will be true for all of the integers greater than or equal to the smallest value proven in the first stage of the argument. So we need to show that the inequality $(1+a)^n>1+na$ implies the inequality $(1+a)^{n+1} > 1+(n+1)a$. |
| Now $(1+a)^{n+1}=(1+a)^n (1+a)$, | We begin by rewriting the power in the desired inequality in terms of the power in the assumed inequality. |
| so the truth of Bernoulli's inequality at value $n$ implies $(1+a)^{n+1} > (1+na)(1+a)$, | This result is based on $(1+a)^n>1+na$, which is Bernoulli's Inequality for value $n$. |
| which implies $(1+a)^{n+1} > 1+(n+1)a+a^2 > 1+(n+1)a$. | We expanded the right hand side of the previous inequality, and since $a^2$ is always positive, we were able to drop the term $a^2$ and obtain a smaller value. |
| Therefore $(1+a)^n>1+na$ is true for all $n\ge 2$. | Having demonstrated the second stage, all the dominoes will have fallen, and therefore the inequality is true for all values of $n\ge 2$. |
We shall show that the sequences $a_n=\left(1+\dfrac{1}{n}\right)^n$ and $b_n=\left(1+\dfrac{1}{n}\right)^{n+1}$ have the same limit, and that limit will be the number $e$. We will do this in three stages.
Proof
| We will first consider the ratio of the two terms. $\dfrac{a_{n+1}}{a_n}=\dfrac{\left(1+\frac{1}{n+1}\right)^{n+1}}{\left(1+\frac{1}{n}\right)^n} =\dfrac{\left(\frac{n+2}{n+1}\right)^{n+1}}{\left(\frac{n+1}{n}\right)^n} =\left(\dfrac{n+2}{n+1}\right)^{n+1}\left(\dfrac{n}{n+1}\right)^{n+1}\left(\dfrac{n+1}{n}\right)^1$ $\qquad\qquad =\left(\dfrac{n^2+2n+1-1}{n^2+2n+1}\right)^{n+1}\left(\dfrac{n+1}{n}\right) =\left(1-\dfrac{1}{(n+1)^2}\right)^{n+1}\left(\dfrac{n+1}{n}\right)$ |
This chain of equalities is primarily obtained through algebraic manipulation. |
| Since $-1<\dfrac{-1}{(n+1)^2} <0$ whenever $n$ is a positive integer, then Bernoulli's Inequality implies $\left(1-\dfrac{1}{(n+1)^2}\right)^{n+1} > 1+(n+1)\left(\dfrac{-1}{(n+1)^2}\right)$. | Use Bernoulli's inequality with $a=\dfrac{-1}{(n+1)^2}$, and exponent $n+1$. |
| Therefore $\dfrac{a_{n+1}}{a_n} > \left(1-\dfrac{1}{n+1}\right)\left(\dfrac{n+1}{n}\right) =\left(\dfrac{n}{n+1}\right)\left(\dfrac{n+1}{n}\right)=1$. | So substituting the result above into our ratio, the statement is now an inequality, and we simplify the right hand side. |
| Since $\dfrac{a_{n+1}}{a_n} >1$, and every term is a positive term, then $a_{n+1} > a_n$. | Thus, we have proven that the sequence is strictly increasing. |
Proof
| Again, we consider a ratio of the two terms. $\dfrac{b_n}{b_{n+1}}=\dfrac{\left(1+\frac{1}{n}\right)^{n+1}}{\left(1+\frac{1}{n+1}\right)^{n+2}} =\dfrac{\left(\frac{n+1}{n}\right)^{n+1}}{\left(\frac{n+2}{n+1}\right)^{n+2}} =\left(\dfrac{n+1}{n}\right)^{n+2}\left(\dfrac{n+1}{n+2}\right)^{n+2}\left(\dfrac{n}{n+1}\right)^1$ $\qquad\qquad =\left(\dfrac{n^2+2n+1}{n^2+2n}\right)^{n+2}\left(\dfrac{n}{n+1}\right) =\left(1+\dfrac{1}{n^2+2n}\right)^{n+2}\left(\dfrac{n}{n+1}\right)$ |
Once again, this chain of equalities is primarily obtained through algebraic manipulation. However, notice that in this ratio, the previous term is in the numerator (unlike the previous ratio). |
| But $0<\dfrac{1}{n^2+2n} <1$ whenever $n$ is a positive integer, so Bernoulli's inequality implies $\left(1+\dfrac{1}{n^2+2n}\right)^{n+2} > 1+(n+2)\left(\dfrac{1}{n^2+2n}\right)$. | Use Bernoulli's Inequality with $a=\dfrac{1}{n^2+2n}$, and exponent $n+2$. |
| Therefore, $\dfrac{b_n}{b_{n+1}} > \left(1+\dfrac{1}{n}\right)\left(\dfrac{n}{n+1}\right) =\left(\dfrac{n+1}{n}\right)\left(\dfrac{n}{n+1}\right)=1$. | Again, we substituted the result above into the ratio, which gave an inequality, and we simplified the right hand side. |
| Since $\dfrac{b_n}{b_{n+1}}>1$, and every term is a positive term, then $b_{n+1} < b_n$. | Thus, we have proven that this sequence is strictly decreasing. |
Proof
| Since $b_n=\left(1+\dfrac{1}{n}\right)^{n+1}=\left(1+\dfrac{1}{n}\right)^n \left(1+\dfrac{1}{n}\right) > \left(1+\dfrac{1}{n}\right)^n = a_n$, | The inequality holds whenever $n$ is a positive integer. |
| then $a_1 < a_2 < \ldots < a_n < \ldots < b_n < \ldots < b_2 < b_1$. | The previous inequality forces each term of $a_n$ to be smaller than each term of $b_n$. |
| Since $a_n$ is an increasing sequence that is bounded above, then it has a least upper bound, so its limit exists. Define $L_1=\lim\limits_{n\to\infty}a_n$. | The sequence $a_n$ is bounded above by $b_1=4$, for example. The Completeness Axiom guarantees the existence of the least upper bound. |
| Similarly, since $b_n$ is a decreasing sequence that is bounded below, then it has a greatest lower bound, so its limit exists. Define $L_2=\lim\limits_{n\to\infty}b_n$. | The sequence $b_n$ is bounded below by $a_1=2$, for example. Although the Completeness Axiom was about least upper bounds, this is an immediate corollary of that assumption. |
| Considering the difference of the two sequences, we have $b_n-a_n=\left(1+\dfrac{1}{n}\right)^{n+1}-\left(1+\dfrac{1}{n}\right)^n$ $\qquad\qquad =\left(1+\dfrac{1}{n}\right)^n \left(1+\dfrac{1}{n}-1\right) = \dfrac{1}{n}a_n$ |
Since we have not yet proven that a gap between $L_1$ and $L_2$ would be impossible, we consider the difference of the sequences. That quantity can be simplified by using the definitions of the two sequences and factoring. |
| But $a_n < b_1$ for every $n$, therefore $0 < b_n-a_n < \dfrac{1}{n}b_1=\dfrac{4}{n}$. | The left hand portion of the inequality occurs from the ordering of the terms of $a_n$ and $b_n$ in the second line of this proof. |
| Thus, by the Sandwich Theorem, we have $0\le \lim\limits_{n\to\infty}(b_n-a_n)\le \lim\limits_{n\to\infty}\dfrac{4}{n}=0$, which implies $L_1=L_2$. | Having been sandwiched, then $\lim\limits_{n\to\infty}(b_n-a_n)=0$. But the Difference Limit Law then gives $\lim\limits_{n\to\infty}b_n - \lim\limits_{n\to\infty}a_n=0$, which is equivalent to $L_1-L_2=0$. So the theorem is true. |
Having proven that the limit exists, we can define the number $e$ to be that limit.
One might note that in the above definition, the values of $n$ were positive integers only. In fact, the statement is still true if $n$ is replaced by any real number $x$ (although the proof would need some modifications). In other words:
The limit theorems we used in the proofs above were sufficient to prove the existence of the limit. If we want to find a decimal approximation for $e$, we need to use a sufficiently large value of $n$ (or $x$). So how large do we need? That depends on how much error we are willing to allow. But these ideas (sufficiently large $n$, amount of error) are intimately related to the definition of the limit. So we now proceed to verify the limit according to the definition (which is really a bit redundant, and may seem somewhat circular, but we want to get a handle on the error in the approximation).
| Suppose $\epsilon>0$ has been provided. Define $M=\dfrac{4}{\epsilon}$. | As in any delta-epsilon proof, the result must be true for any possible epsilon. And epsilon plays the role of the error tolerance we discussed above. The quantity $M$ is defined in terms of epsilon, and will be larger if the error needs to be smaller. But note that $M>0$. |
| Then for all $x$, the inequality $n>M$ implies | Here is the beginning of the chain of implications |
| $n>\dfrac{4}{\epsilon}$, so $\dfrac{4}{n} < \epsilon$. | We replaced $M$ according to its definition, then solved the inequality for epsilon. |
| Now when $a_n=\left(1+\dfrac{1}{n}\right)^n$ and $b_n=\left(1+\dfrac{1}{n}\right)^{n+1}$, we have $a_n < e < b_n$. | These were the sequences we used in the proof above. The inequality is true because $a_n$ was an increasing sequence with limit $e$, and $b_n$ was a decreasing sequence with limit $e$. |
| Thus $\left|\left(1+\dfrac{1}{n}\right)^n-e\right| < b_n-a_n < \dfrac{4}{n} < e$, | The first inequality may be obtained by subtracting $a_n$ from each expression in the previous result. The second inequality was determined in the previous proof above. |
| and therefore $\lim\limits_{n\to\infty}\left(1+\dfrac{1}{n}\right)^n=e$. | And the theorem is proved. |
Therefore, if we want an approximation of $e$ accurate to within a value $\epsilon$, we need to choose a value $n$ for which $n > \dfrac{4}{\epsilon}$. So, for example, to obtain a value guaranteed to be accurate to five decimal places, we would need $\epsilon=10^{-5}$, and this implies $n > 4\times 10^5$ (i.e. 400,000). Using this approach, we learn that $e\approx 2.71828$. Although using this limit to approximate $e$ is mathematically valid, we might notice that the large exponents required render it somewhat impractical, even with computer technology to do the computations. There are other approaches to finding a value of $e$ that obtain the result with much less effort, and each can be proven to be an implication of this definition.