We use MathJax

Variations on the Limit Definition

Several different varieties of limits exist. On this page, we collect them all.

The Original (Two-Sided) Limit

• The expression   $\lim\limits_{x\to c} f(x)=L$   means: For every   $\epsilon >0$,   there exists a   $\delta >0$,   such that for every $x$, the expression   $0 < |x-c| < \delta$   will imply   $|f(x)-L| < \epsilon$.

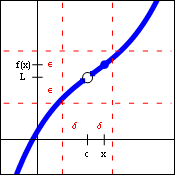
This is the basic two-sided limit that we described on a previous page. If a limit exists but the point does not, then the function has a hole (as pictured above). If both the limit and the point exist, the function may still have a hole, if the point is located somewhere else (above or below the hole). And if the limit and the point both exist, and the point is located at the same location given by the limit, then the function is said to be continuous at that point.

One-Sided Limits

• The expression   $\lim\limits_{x\to c+} f(x)=L$   means: For every   $\epsilon >0$,   there exists a   $\delta >0$,   such that for every $x$, the expression   $c < x < c+\delta$   will imply   $|f(x)-L| < \epsilon$.
• The expression   $\lim\limits_{x\to c-} f(x)=L$   means: For every   $\epsilon >0$,   there exists a   $\delta >0$,   such that for every $x$, the expression   $c-\delta < x < c$   will imply   $|f(x)-L| < \epsilon$.

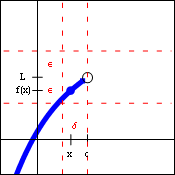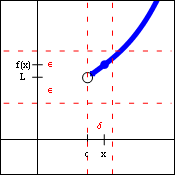
$\lim\limits_{x\to c+} f(x)=L$	$\lim\limits_{x\to c-} f(x)=L$

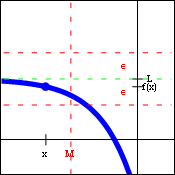
These forms allow us to describe the behavior of a function from one side only. The first limit is often described as approaching the value $c$ from the right, and the second limit is often described as approaching $c$ from the left. Both of these forms will obey the generic limit laws and the limit inequalities.

One-sided limits are critically important when the domain of the function is only on one side of the limit point, as in the function   $f(x)=\sqrt{x}$.   They also allow us to describe different limiting behaviors on the two sides of the limit point, as in the function   $f(x)=\dfrac{|x|}{x}$.

Limits at Infinity

• The expression   $\lim\limits_{x\to \infty} f(x)=L$   means: For every   $\epsilon >0$,   there exists a   $M>0$,   such that for every $x$, the expression   $x>M$   will imply   $|f(x)-L| < \epsilon$.
• The expression   $\lim\limits_{x\to -\infty} f(x)=L$   means: For every   $\epsilon >0$,   there exists a   $M<0$,   such that for every $x$, the expression   $x < M$   will imply   $|f(x)-L| < \epsilon$.

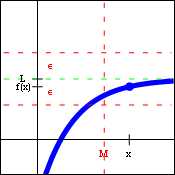
$\lim\limits_{x\to \infty} f(x)=L$	$\lim\limits_{x\to -\infty} f(x)=L$

Limits at infinity are very useful when testing and describing horizontal asymptotes. That is to say, the limit statement   $\lim\limits_{x\to \infty} f(x)=L$   implies that the function $f(x)$ has the line   $y=L$   as a horizontal asymptote. Functions may have zero, one, or two horizontal asymptotes, since the behavior on the left and right ends of the graph need not be identical. Both of these forms obey the generic limit laws and the limit inequalities.

Infinite Limits

• The expression   $\lim\limits_{x\to c} f(x)=\infty$   means: For every   $B >0$,   there exists a   $\delta >0$,   such that for every $x$, the expression   $0 < |x-c| < \delta$   will imply   $f(x)>B$.
• The expression   $\lim\limits_{x\to c} f(x)=-\infty$   means: For every   $B < 0$,   there exists a   $\delta >0$,   such that for every $x$, the expression   $0 < |x-c| < \delta$   will imply   $f(x) < B$.

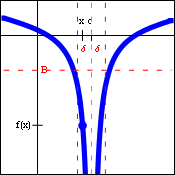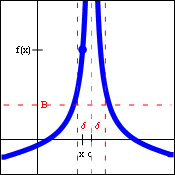
$\lim\limits_{x\to c} f(x)=\infty$	$\lim\limits_{x\to c} f(x)=-\infty$

Infinite limits are useful when testing and describing vertical asymptotes. In other words, the limit statement   $\lim\limits_{x\to c} f(x)=\infty$  implies that the function $f(x)$ has the line   $x=c$   as a vertical asymptote. There is no restriction on the number of vertical asymptotes that a functions may have. However, since the "answer" to these limits (infinity or negative infinity) is not a real number, these limits actually do not exist. Because of that, the generic limit laws and the limit inequalities cannot be applied to infinite limits. However, the ability to use infinity as an answer (rather than "does not exist") does help describe a specific behavior of the function.

One-Sided Infinite Limits

• The expression   $\lim\limits_{x\to c+} f(x)=\infty$   means: For every   $B >0$,   there exists a   $\delta >0$,   such that for every $x$, the expression   $c < x < c+\delta$   will imply   $f(x)>B$.
• The expression   $\lim\limits_{x\to c+} f(x)=-\infty$   means: For every   $B < 0$,   there exists a   $\delta >0$,   such that for every $x$, the expression   $c < x < c+\delta$   will imply   $f(x) < B$.
• The expression   $\lim\limits_{x\to c-} f(x)=\infty$   means: For every   $B >0$,   there exists a   $\delta >0$,   such that for every $x$, the expression   $c-\delta < x < c$   will imply   $f(x)>B$.
• The expression   $\lim\limits_{x\to c-} f(x)=-\infty$   means: For every   $B < 0$,   there exists a   $\delta >0$,   such that for every $x$, the expression   $c-\delta < x < c$   will imply   $f(x) < B$.

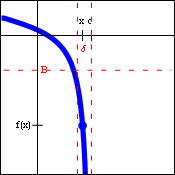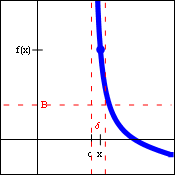
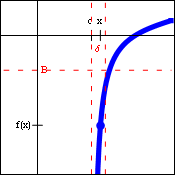
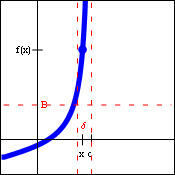
$\lim\limits_{x\to c+} f(x)=\infty$	$\lim\limits_{x\to c+} f(x)=-\infty$	$\lim\limits_{x\to c-} f(x)=\infty$	$\lim\limits_{x\to c-} f(x)=-\infty$

Quite often, a function will have a vertical asymptote, but head off in different directions on the two sides of that asymptote. When that is the case, the limit description of the situation requires one-sided infinite limits. As before, since the "answer" to these limits (infinity or negative infinity) is not a real number, these limits actually do not exist. Because of that, the generic limit laws and the limit inequalities cannot be applied to these limits either. However, the ability to use infinity as an answer (rather than "does not exist") does help describe a specific behavior of the function.