
We use MathJax
There are a few very important limits which cannot be handled easily by our previous theorems, and therefore require delta-epsilon proofs to establish. We discuss these limits here.
Show that $\lim\limits_{x\to\infty}\dfrac{1}{x}=0$.
| Suppose $\epsilon>0$ has been provided. | As always, every delta-epsilon proof must work for an arbitrary epsilon. |
| Define $M=\dfrac{1}{\epsilon}$. Note that $M>0$. | For any epsilon, in a limit at infinity we must exhibit the value $M$ for which the argument will be true. |
| Then for all $x$, the inequality $x>M$ implies | This is the inequality in a limit at infinity that begins the chain of implications. |
| $x>\dfrac{1}{\epsilon}$, $\dfrac{1}{x}<\epsilon$, |
First, we replace $M$ according to its definition. Then taking reciprocals of both sides, we note that the reciprocal function is decreasing, therefore the inequality signs change directions. |
| and since $x > M > 0$, we also have $\dfrac{1}{x} > 0 > -\epsilon$, | Here, we establish the relationship between $\dfrac{1}{x}$ and $-\epsilon$. |
| $-\epsilon < \dfrac{1}{x} < \epsilon$, and finally $\left|\dfrac{1}{x}-0\right| < \epsilon$. |
Then, we can obtain the absolute value inequality necessary to conclude with the limit statement. |
| Therefore, $\lim\limits_{x\to\infty}\dfrac{1}{x}=0$. | And the proof is complete. |
Show that when $b>1$, then $\lim\limits_{x\to\infty}b^{-x}=0$.
| Suppose $\epsilon>0$ has been provided. | Once again, we begin with an arbitrary epsilon. |
| Define $\epsilon_2=\min\{\epsilon,0.9\}$. | The new epsilon allows us to avoid complications arising from too large an original epsilon. |
| Define $M=\log_b\dfrac{1}{\epsilon_2}$. Note that $M>0$. | Since $\epsilon_2<1$ and $b>1$, then $M$ will be positive. |
| Then for all $x$, the inequality $x>M$ implies $x>\log_b\dfrac{1}{\epsilon_2}$, so | This begins the chain of implications. |
| $b^x>\dfrac{1}{\epsilon_2}$, $\dfrac{1}{b^x}<\epsilon_2$, |
First, we exponentiate both sides. Since $b>1$, this is an increasing function, and the inequality sign does not change its direction on this step. Then, we take reciprocals of both sides. Reciprocals of positive quantities will cause the inequality to change directions. |
| $-\epsilon_2 < 0 < b^{-x} < \epsilon_2$, and $|b^{-x}-0| < \epsilon_2 < \epsilon$. |
Here, we have rewritten the reciprocal using a negative exponent, and noted that it was positive, and therefore greater than a negative quantity. That allowed us to set up the inequality. |
| Therefore, when $b>1$ we have $\lim\limits_{x\to\infty}b^{-x}=0$. | And we have completed the proof. |
Show that $\lim\limits_{\theta\to 0}\dfrac{\sin\theta}{\theta}=1$.
Consider the following diagram, where $BC$ is an arc of a unit circle centered at the origin.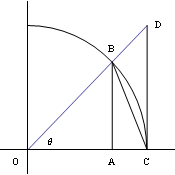 |
We shall use this diagram to suggest some relationships involving the value of $\theta$. However, since we are using the diagram, the relationships will only be valid for $0 < \theta < \dfrac{\pi}{2}$. |
| Point $B$ is on the unit circle, and therefore its coordinates are $(\cos\theta,\sin\theta)$. Thus $AB=\sin\theta$ and $OA=\cos\theta$. Point $C$ is also on the unit circle, so its coordinates are $(1,0)$. By similar triangles, we find the coordinates of point $D$ to be $(1,\tan\theta)$. | Point $B$ is an immediate consequence of the definition of the trig functions. The similar triangles used for point $D$ were $\triangle OAB$ and $\triangle OCD$. |
| Now $\text{Area }\triangle OBC < \text{Area sector }OBC < \text{Area }\triangle OCD$, | These three objects are nested within one another in the diagram, so the area statements must follow. |
| so we have $\dfrac12 (1)\sin\theta < \dfrac{\theta}{2\pi}(\pi 1^2) < \dfrac12 (1)\tan\theta$, | For a triangle $\text{Area }=\dfrac12 bh$, and for a sector it is a fraction of the area of a circle. |
| which gives $1 < \dfrac{\theta}{\sin\theta} < \dfrac{1}{\cos\theta}$. | We multiplied each quantity by $\dfrac{2}{\sin\theta}$, which is a positive quantity when $0 < \theta < \dfrac{\pi}{2}$. |
| Taking reciprocals, we obtain $1 > \dfrac{\sin\theta}{\theta} > \cos\theta$. | Since all of the quantities are positive, the reciprocal function is strictly decreasing, and the inequality signs reverse direction. |
| Then $\lim\limits_{\theta\to 0+} 1\ge \lim\limits_{\theta\to 0+}\dfrac{\sin\theta}{\theta} \ge \lim\limits_{\theta\to 0+}\cos\theta$, which gives $1\ge \lim\limits_{\theta\to 0+}\dfrac{\sin\theta}{\theta} \ge 1$. | We can take limits of each expression. |
| Therefore $\lim\limits_{\theta\to 0+}\dfrac{\sin\theta}{\theta} = 1$. | We successfully sandwiched the function $\dfrac{\sin\theta}{\theta}$ for values where $0 < \theta < \dfrac{\pi}{2}$. |
| But $\dfrac{\sin\theta}{\theta}$ is an even function, thus $\lim\limits_{\theta\to 0-}\dfrac{\sin\theta}{\theta} = 1$ also. | The function $\dfrac{\sin\theta}{\theta}$ is even, since $\dfrac{\sin(-\theta)}{-\theta}=\dfrac{-\sin\theta}{-\theta}=\dfrac{\sin\theta}{\theta}$. |
| and therefore $\lim\limits_{\theta\to 0}\dfrac{\sin\theta}{\theta} = 1$. | Since the two one-sided limits were equal, the two-sided limit exists as well. |