
We use MathJax
In elementary algebra, the slope of a line was introduced through the definition $m=\dfrac{y_2-y_1}{x_2-x_1}$. Every line had a constant slope all along its length. And from this definition of the slope, we were able to write the equation of a line $y-y_1=m(x-x_1)$. You might notice that this second equation is essentially identical to the first, by multiplying both sides by the denominator, and removing the subscript 2.
We would also like to be able to talk about the slope of a curve, but we will have to realize that the slope is not the same at different points on the curve. However, it seems intuitively obvious that the slope of the curve at a particular point ought to equal the slope of the tangent line along that curve. This is displayed in the graph below. In fact, this is how a tangent line will be defined.
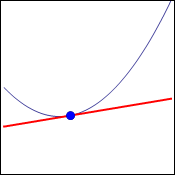
To find the slope of a line, we typically have two points that we substitute into the formula $m=\dfrac{y_2-y_1}{x_2-x_1}$. But with a tangent line, we have only one point. If we try to substitute the same point twice, we will arrive at the form $\dfrac00$, which we know to be undefined. However, we have had a lot of practice with limits, and we know that even if a function is not defined at a point, it may have a limit at that point.
So here is how we can "approach" that tangent line as a limit. We will start with the same curve and the same point, but add a second point on the curve some distance away from the original point. The line that is drawn through those two points is called a secant line.
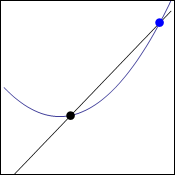
Now, we can allow the second point (blue in the image) to approach the first point (black in the image), and we see that the secant lines do approach the tangent line. The animation below also shows us that the same tangent line is obtained whether the point is approaching from the right or the left.
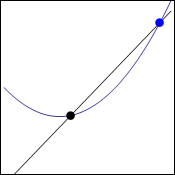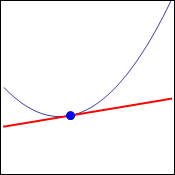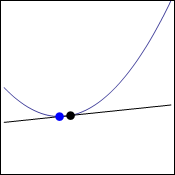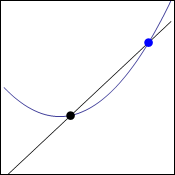
We know how to find the slope of a secant line, namely $m=\dfrac{y_2-y_1}{x_2-x_1}$. In function notation, this becomes $m=\dfrac{f(x_2)-f(x_1)}{x_2-x_1}$. Then, we want the value $x_2$ to approach the value $x_1$, as this would cause the point $(x_2,y_2)$ to approach the point $(x_1,y_1)$. So the slope of the tangent line would be $m=\lim\limits_{x_2 \to x_1}\dfrac{f(x_2)-f(x_1)}{x_2-x_1}$. This is a little messier than the formula usually provided. To clean it up, we use the substitutions $x_2=x+h$ and $x_1=x$. Geometrically, this makes $h$ the horizontal distance between the two points, and $x$ is the $x$-coordinate of the point on the tangent line. Then we have the following definition of the slope of a tangent line.
Then, once we have the slope and a point, we can write the equation of the tangent line using the point-slope form of the line: $y-y_1=m(x-x_1)$.
There are some situations when the limit may not exist. These either correspond to a vertical tangent line (where the slope is undefined), or to no tangent line at all (because of some other behavior in the graph such as a discontinuity or a corner).
| Since $f(6)=3(6^2)-4(6)+5=89$, the point on the tangent line is $(6,89)$. | To find the equation of a line, we need a point and a slope. Here, we have found the coordinates of the point. |
| Then $m=\lim\limits_{h\to 0}\dfrac{f(6+h)-f(6)}{h}$, which gives | Then we use the definition of the slope of the tangent line. Notice that we have substituted in the $x$-coordinate of the point first. |
| $m=\lim\limits_{h\to 0}\dfrac{3(6+h)^2-4(6+h)+5-89}{h}$, which simplifies to | Then, we use the given function, $f(x)=3x^2-4x+5$, to evaluate $f(6+h)$. Notice that we already had the answer to $f(6)$. |
| $m=\lim\limits_{h\to 0}\dfrac{108+36h+3h^2-24-4h+5-89}{h}$ $\qquad =\lim\limits_{h\to 0}\dfrac{3h^2+32h}{h}$ |
Then we expanded the numerator and combined like terms. |
| $m=\lim\limits_{h\to 0}\dfrac{h(3h+32)}{h}$ $\qquad =\lim\limits_{h\to 0}(3h+32)$ |
We then factor the numerator, and divide out the common factor. |
| $m=3(0)+32=32$ | Then we can evaluate the limit by substitution. Therefore, the slope of the tangent line is 32. |
| Thus we have $y-89=32(x-6)$, and therefore the equation of the tangent line is $y=32x-103$. | We substituted the slope and the point into the equation $y-y_1=m(x-x_1)$, and then solved for $y$. |