Taylor Polynomials

In each graph, the red curve is the function for which Taylor polynomials have been computed, the black curves are the Taylor polynomials, and the number in the display is the degree of the Taylor polynomial.

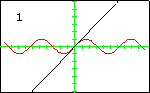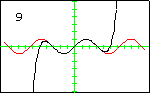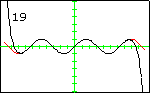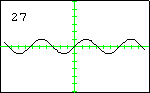The Sine Function

The first 14 Taylor polynomials at $x=0$ are displayed here. The sequence of Taylor polynomials will converge to the sine function at all real numbers. Since the sine function is an odd function, each Taylor polynomial is also an odd function.

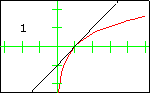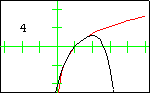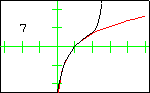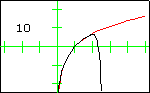Taylor polynomials approaching the logarithm function.

The Natural Logarithm Function

The first 10 Taylor polynomials at $x=1$ are displayed here. Since the logarithm function has a discontinuity at $x=0$, the radius of convergence of the sequence of Taylor polynomials is 1. That is, the Taylor polynomials approach the logarithm function only on the interval $(0,2)$. Outside that interval, no convergence occurs.

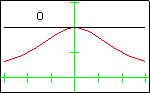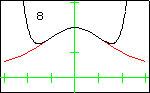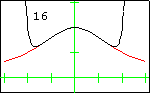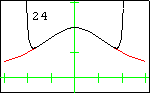The Witch of Agnesi

The Witch of Agnesi displayed here has the equation $y=\dfrac{8}{x^2+4}$. The first 13 Taylor polynomials at $x=0$ are displayed. Although the function is defined for all real numbers, its sequence of Taylor polynomials does not converge for all real numbers. The radius of convergence is 2, so convergence only occurs on the interval $(-2,2)$. This is due to the fact that zeros of the denominator occur at the complex values $2i$ and $-2i$.