
We use MathJax
What is $\sqrt{-1}$ ? A symbol thrust upon earthlings by an alien culture? Well, not quite... (unless you view mathematics as representative of an alien culture... but we won't go there).
The "usual" numbers "normal" people work with are called real numbers. They include whole numbers, fractions, decimals, negative numbers, square roots of positive numbers, and numbers like pi (3.14159265...). They include basically anything that a calculator will turn into a decimal, or anything that has a position on the number line.
But $\sqrt{-1}$ does not have a position on the number line. There is no number we can square to get negative one. Squaring a positive number always produces a positive number, and squaring a negative number also always produces a positive number. So how do we square a number to get a negative one?
Answer: We can't use a real number for $\sqrt{-1}$. We must use a different kind of number. The sixteenth century mathematicians who first seriously worked with $\sqrt{-1}$ weren't sure what its significance was, so they called it an imaginary number, a very unfortunate term. In fact, there is nothing imaginary about $\sqrt{-1}$. (But it did take two centuries before mathematicians generally understood its significance.)
Today, we often use the symbol $i$ to represent $\sqrt{-1}$. Mathematicians usually use one of two statements as the definition of $i$, either $i = \sqrt{-1}$ or $i^2 = -1$. (Some electrical engineers will use $j$ instead of $i$, because they use $i$ to represent inductive force, alias current. But the idea is the same.)
We don't need any other definitions for square roots of other numbers, having $i$ is enough. For instance, we can write $\sqrt{-9} = 3i$, since the square root of 9 is 3, and the square root of a negative number will produce the number $i$.
The collection of numbers created by taking square roots of the negative numbers are sometimes called the pure imaginary numbers. In symbols, we might write a generic pure imaginary number as $bi$, the product of a nonzero real number $b$ with the imaginary number $i$. None of the pure imaginary numbers have a position on the number line.
We can also talk about adding a real number with a pure imaginary number. The result is called a complex number. In symbols, complex numbers are numbers of the form $a+bi$, where $a$ is a real number, and $bi$ is a pure imaginary number.
If these numbers aren't on the number line, can we draw pictures of complex or imaginary numbers? Actually, yes. But a one-dimensional number line will not sufficient. The pure imaginary part of the complex number needs to be represented on a second number line. In other words, we need a two-dimensional picture to represent complex numbers. Here is a picture of the number $2+3i$, represented by a point.
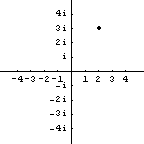
So the real numbers are points on the horizontal axis. Imaginary numbers are those numbers which are not real, and are located somewhere other than the horizontal axis. Pure imaginary numbers are points on the vertical axis (other than the origin). Complex numbers include all possible points in the picture. (Real numbers are complex numbers. So are imaginary numbers. Just like a whole number is also a fraction.)
Couldn't this go on forever? What about $\sqrt{i}$, for instance? Won't we need a $j$, or some other invention (er, dimension)? Well..., you can take everything to extremes, but we won't need to. It turns out that the Square Root of i is another complex number. We won't need a $j$. We won't need a third dimension for $\sqrt{i}$.