Basic Counting

Combinatorics is the study of counting the number of ways events can happen. Since such results are often quite large, we do not want to list all of the possibilities and count them one by one. Combinatorics will provide various rules and formulas for more quickly determining results.

Stages and the Multiplication Rule

Suppose an event comes in two stages. The number of ways the first stage can occur is the number $m$, and the number of ways the second stage can occur is $n$. Then the event consisting of the two stages together can occur in $mn$ ways.

Tom has 5 shirts and 4 pairs of pants. He has a total of $5\times 4=20$ ways of choosing an outfit. (A tree diagram can show all of the possibilities, and help explain the multiplication.)

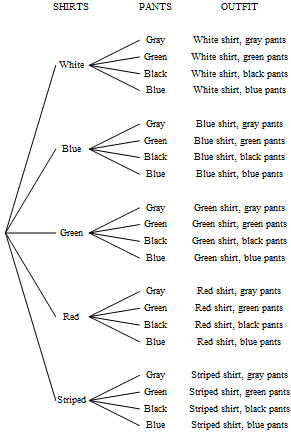
The Multiplication Rule can be generalized to any number of stages.

For the local boosters club, 3 people are running for the office of president, 2 for secretary, and 4 for treasurer. There are $3\times 2\times 4=24$ ways for the offices to be filled.

Sometimes the stages appear to be identical, but each stage should be considered distinct.

Three dice are rolled. There are $6\times 6\times 6=6^3=216$ possible outcomes. (You may need to imagine that each of the dice is a different color to understand the result.)
Four different door prizes are to be awarded in a group of 30 people, and each person could win more than one prize. There are $30^4=810000$ ways to award the prizes.

And sometimes the choices in each stage are "yes" and "no", whether a particular item is included or not.

Tony's Sub Shop offers salami, chicken, lettuce, tomato, and peppers for their sub sandwiches. There are $2\times 2\times 2\times 2\times 2 =2^5=32$ different sandwiches that can be created. (Each item creates a "yes" or "no" response. Note that one of the outcomes consists of five "no" responses, which would be a sandwich consisting only of bread. If that outcome is to be avoided, then there are just 31 different sandwiches.)
A set consists of 7 elements. There are $2^7=128$ subsets of the set. (This includes the empty set and the original set as subsets. In general, a set of $n$ elements has $2^n$ subsets.)

There is always a certain assumption of order in the Multiplication Rule. In each of the examples above, there was a first stage to the event, and a second stage, and so on.

Arrangements and the Permutation Rule

A permutation is an arrangement of a set of objects. A set of $n$ objects can be arranged in $n!$ ways. The Permutation Rule is a special case of the Multiplication Rule, where the each stage of a decision always has one less possibility than the previous stage.

Five children (Al, Bob, Cathy, Don, Ed) can line up in $5\times 4\times 3\times 2\times 1=5!=120$ ways. (There are 5 possibilities for who goes first. Once the first child is selected, there are only four possibilities for the second child. Once the first two are known, there are only three possibilities for the third child. And so on.)
The letters in the word "SYNTAX" can be arranged in $6!=720$ ways.

Arrangements are usually assumed to be linear, and the line has an order (a front of the line, and a back of the line). If there is no front or back, but only a center of the arrangement, the Permutation Rule result will have to be divided by the number of rotational symmetries in the arrangement. (If the distinction between left and right is also ignored, then the denominator will be twice as large.)

If a line has no front or back, then five children can line up in $\dfrac{5!}{2}=60$ ways. (That is, the order Al-Bob-Cathy-Don-Ed is the same as Ed-Don-Cathy-Bob-Al, which would result if each child rotates to face the opposite direction.)
Five children can form a circle in $\dfrac{5!}{5}=24$ ways. (A circle has as many symmetries as there are objects in the circle, since any particular position in the circle could be "first".)
Six desks are arranged in 2 rows and 3 columns. Six children can seat themselves in these desks in $6!=720$ ways. (The desks typically face the front of a room, which breaks any possible symmetry.)
Six children arrange themselves into 2 rows and 3 columns, where no front or back is assumed. There will be $\dfrac{6!}{2}=360$ possible arrangements. (A rectangle rotated 180 degrees about its center will land upon itself.)
Nine children arrange themselves into 3 rows and 3 columns, where no front or back is assumed. There are $\dfrac{9!}{4}=90720$ possible arrangements. (A square rotated 90 degrees about its center will land upon itself.)

Distinguishable Permutations and the Multinomial Coefficient

When the set contains some objects that are identical (or at least indistinguishable according to a certain characteristic), then the number of permutations must be divided by the number of ways the identical objects could be arranged. In other words, if a set has $n$ objects of $k$ different types, with $n_1$ of the first type, $n_2$ of the second type, etc., then there are $\dbinom{n}{n_1,n_2,\ldots,n_k}=\dfrac{n!}{n_1!\times n_2!\times\ldots\times n_k!}$ distinguishable permutations of that set.

One green, one white, one black, and four red balls can be arranged in $\dfrac{7!}{4!}=210$ ways. (There are seven balls, but the four red balls are indistinguishable from one another. We could have included "one factorial" in the denominator three times as indicated by the formula, but that would not have changed the result.)
The letters in the word "MISSISSIPPI" can be arranged in $\dfrac{11!}{4!\times 4!\times 2!} = 34650$ ways. (There are 4 I's, 4 S's, and 2 P's among the 11 letters. Identical letters are indistinguishable.)
A group of 14 people is to be partitioned into two subgroups of 4 and two subgroups of 3. There are $\dfrac{14!}{4!\times 4!\times 3!\times 3!} = 4204200$ possible ways to partition the group. (Partitioning a group is equivalent to treating the members of each subgroup as indistinguishable.)
In the expansion of the algebraic expression $(w+x+y+z)^{17}$, the coefficient of the $w^3x^4y^5z^5$ term will be the multinomial coefficient $\dbinom{17}{3,4,5,5}=\dfrac{17!}{3!\times 4!\times 5!\times 5!} = 171531360$. (In other words, this is the number of ways to arrange the letters in the word "wwwxxxxyyyyyzzzzz", which is equivalent to identifying from which of the seventeen factors each variable will be extracted.)

Permutations of a Subset

Sometimes only the first few items in the arrangement are important, and the rest can be ignored. That is, the number of permutations of $n$ objects taken $r$ at a time is ${}_n P_r = \dfrac{n!}{(n-r)!}$. This is really a special case of the Distinguishable Permutation Rule.

Four different door prizes are to be awarded in a group of 30 people, where no person wins more than one prize. There are ${}_{30} P_4 = \dfrac{30!}{26!}=30\times 29\times 28\times 27 = 657720$ ways to award the prizes. (The 26 "losers" are essentially indistinguishable.)

Choices and the Combination Rule

When items are selected or chosen from a set, essentially two groups are being identified. One group consists of those items chosen, and the other group are the items not chosen. When the order of the items chosen is irrelevant, the selection is called a combination. There are ${}_n C_r = \dbinom{n}{r} = \dfrac{n!}{r!(n-r)!}$ combinations of $n$ objects taken $r$ at a time. This result is also a special case of the Distinguishable Permutation Rule.

Four different individuals in a group of 30 people are selected for a committee. There are ${}_{30} C_4=\dbinom{30}{4}=\dfrac{30!}{4!\times 26!}=27405$ possible committees. (The four chosen for the committee are essentially "indistinguishable", in that it doesn't matter when they were chosen. And the 26 not chosen for the committee are also treated as indistinguishable.)
A poker hand consists of 5 cards from a deck of 52 cards. There are ${}_{52} C_5=\dbinom{52}{5}=\dfrac{52!}{5!\times 47!}=2598960$ possible poker hands.
Tom travels in a city whose streets form a rectangular grid from one point to another 3 blocks north and 5 blocks west. There are ${}_8 C_3=\dbinom{8}{3}=\dfrac{8!}{3!\times 5!}=56$ ways to travel the 8 blocks. (This is equivalent to arranging the letters of the path "NNNWWWWW", which is equivalent to choosing when to travel each block north.)
In the expansion of the algebraic expression $(x+y)^{17}$, the coefficient of the $x^6 y^{11}$ term will be the binomial coefficient ${}_{17} C_6=\dbinom{17}{6}=\dfrac{17!}{6!\times 11!} =12376$. (This is equivalent to choosing 6 factors in which to extract the variable $x$, leaving the other 11 factors to provide the variable $y$.)