Geometric Sequences

Once again, we consider the situation of a sequence described by a list of numbers. This time, however, our pattern will involve multiplication rather than addition.

Common Ratios and Geometric Sequences

Consider the sequence $14, 42, 126, 378, 1134, \ldots$ After some thought, we might notice that each term is always a constant multiple of the previous term. That is, the ratio of consecutive terms is a constant. If we write the ratios in a row underneath the spaces between the terms, we obtain the following diagram.

\begin{equation*} \begin{array}{ccccccccc} 14, & \phantom. & 42, & \phantom. & 126, & \phantom. & 378, & \phantom. & 1134,\ldots \\ \phantom. & \times 3 & \phantom. & \times 3 & \phantom. & \times 3 & \phantom. & \times 3 & \phantom. \end{array} \end{equation*}

Whenever a term of a sequence is a constant multiple of the preceding term, the sequence is called a geometric sequence. The ratio between consecutive terms is called the common ratio, and is often identified by the variable $r$.

In our specific example, the common ratio $r=3$. This pattern immediately implies that the recursive formula is $a_n=3a_{n-1},\quad a_1=14$. Furthermore, we see that the second term was produced by multiplying by one factor of three, the third term was produced by multiplying by two factors of three, and in general the $n$th term is produced by multiplying by a total of $n-1$ factors of three. Therefore, the explicit formula is $a_n=14(3^{n-1})$.

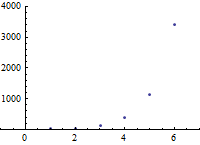
graph of the sequence a sub n equals 3 times a sub n minus 1, a sub 1 equals 14

In general, the recursive formula of a geometric sequence always has the form $a_n=r(a_{n-1})$, and the explicit formula always has the form $a_n=a_1 r^{n-1}$. In particular, the explicit formula of a geometric sequence will always be exponential, as is implied in the graph above, and it will consist of a single term.

The geometric sequence is also used in a variety of applications. Examples include:

Tim's starting salary is $\$24,000$ per year, and he receives a $5\%$ cost of living raise each year. This is a geometric sequence with first term $24000$ and common difference $1.05$.
Campbell County's population was $42,000$ in 1990, and since then has been increasing by $1\%$ each year. This is a geometric sequence with first term $42000$ and common difference $1.01$.
Karen deposited $\$7000$ in her account, and the bank is paying her $6\%$ interest compounded monthly. This is a geometric sequence with first term $7000$ and common difference $1.005$.

Epilogue

Common differences and common ratios are the two easiest situations, and both arithmetic and geometric sequences have many practical applications. If, however, there is neither a common difference nor a common ratio, it may be that a second row will contain a pattern. See the page Recognizing More Patterns for more information.