A Gallery of Exponential, Logarithmic, and Hyperbolic Functions

Exponential functions have variables appearing in the exponent. Also on this page are logarithmic functions (which are inverses of exponential functions) and hyperbolic functions (which are combinations of exponential functions). Each of the graphs on this page is displayed in the window $[-5,5]\times[-5,5]$.

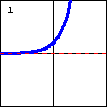	$y=e^x$ Here is a basic exponential function. Any relationship where the rate of growth is determined by the amount present will be exponential. Unrestricted population growth and continuously compounded interest are two examples.
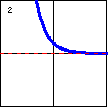	$y=\left(\dfrac{1}{e}\right)^x=e^{-x}$ When the base is between 0 and 1, a decreasing exponential function results. Radioactive decay is an example.
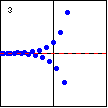	$y=(-e)^x$ If one attempts to use a negative base in an exponential function, points will be scattered along two curves, and a great many more values of the function will be undefined.
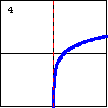	$y=\ln x$ The logarithmic function is the inverse of the exponential function.
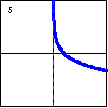	$y=\log_{1/e} x=-\ln x$ Here is a logarithmic function with a base between 0 and 1.
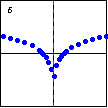	$y=\log_{-e} x$ If one attempts to use a negative base in a logarithmic function, points will be scattered along two curves (both asymptotic to the $y$-axis), and a great many more values of the function will be undefined.
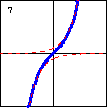	$y=\sinh x=\dfrac{e^x-e^{-x}}{2}$ The hyperbolic sine function is asymptotic to a pair of exponential functions.
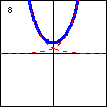	$y=\cosh x=\dfrac{e^x+e^{-x}}{2}$ The hyperbolic cosine function is also asymptotic to a pair of exponential functions. This function is also known as a catenary, which is the shape taken by a chain suspended between two points.
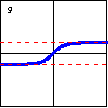	$y=\tanh x=\dfrac{e^x-e^{-x}}{e^x+e^{-x}}$ This is the graph of the hyperbolic tangent function.
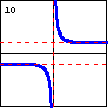	$y=\coth x=\dfrac{e^x+e^{-x}}{e^x-e^{-x}}$ This is the graph of the hyperbolic cotangent function.
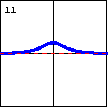	$y=\operatorname{sech} x=\dfrac{2}{e^x+e^{-x}}$ This is the graph of the hyperbolic secant function.
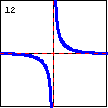	$y=\operatorname{csch} x=\dfrac{2}{e^x-e^{-x}}$ This is the graph of the hyperbolic cosecant function.
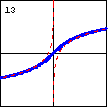	$y=\operatorname{arcsinh} x=\ln\left(x+\sqrt{x^2+1}\right)$ The inverse hyperbolic sine function is asymptotic to a pair of logarithmic functions.
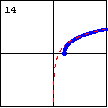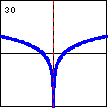
	$y=\operatorname{arccosh} x=\ln\left(x+\sqrt{x^2-1}\right)$ The graph of the inverse hyperbolic cosine function is identical to half of a rotated catenary curve, and is asymptotic to a logarithmic function.
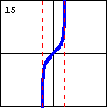	$y=\operatorname{arctanh} x=\dfrac12 \ln\left(\dfrac{1+x}{1-x}\right)$ Here is the graph of the inverse hyperbolic tangent function.
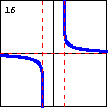	$y=\operatorname{arccoth} x=\dfrac12 \ln\left(\dfrac{x+1}{x-1}\right)$ Here is the graph of the inverse hyperbolic cotangent function.
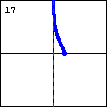	$y=\operatorname{arcsech} x=\ln\left(\dfrac{1}{x}+\sqrt{\dfrac{1}{x^2}-1}\right)$ The inverse of the hyperbolic secant required a restriction of the range in order to remain a function.
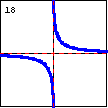	$y=\operatorname{arccsch} x=\ln\left(\dfrac{1}{x}+\sqrt{\dfrac{1}{x^2}+1}\right)$ Here is the inverse hyperbolic cosecant function.
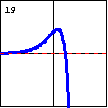	$y=3e^x-e^{2x}$ Besides hyperbolic sines and cosines, the addition of exponential functions can create curves of this type.
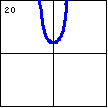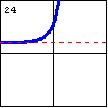
	$y=e^{x^2}$ Here is an exponential function with a quadratic exponent. Other even exponents will create a similar graph.
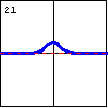	$y=e^{-x^2}$ This exponential function is related to the normal curve of statistics.
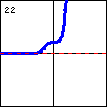	$y=e^{x^3}$ Here is an exponential function with a cubic exponent. Other odd exponents will create a similar graph.
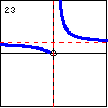	$y=e^{x^{-1}}=e^{1/x}$ When the reciprocal function is used in an exponential function, two branches will result.
	$y=e^{e^x}$ Composition of an increasing exponential function with itself creates a faster growing function.
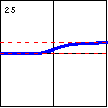	$y=e^{-e^{-x}}$ Composition of a decreasing exponential function with itself creates a population growth curve known as the Gompertz curve.
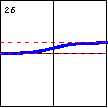	$y=\dfrac{1}{1+e^{-x}}$ This function results from a fairly simple differential equation that models population growth with an environmental maximum.
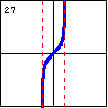	$y=\dfrac{1}{1-e^x}$ Changing the signs of the previous function will have a significant impact on the graph.
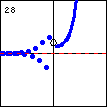	$y=x^x$ This curve is continuous for positive values, but for negative values points will be scattered along two curves, and a great many more negative values of the function will be undefined.
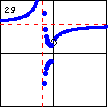	$y=\left(1+\dfrac{1}{x}\right)^x$ This function is sometimes used as part of the definition of the number $e$. On the interval $[-1,0]$, points are scattered along two curves, with many undefined values of the function.
	$y=\ln \|x\|$ This function is often encountered as the integral of the reciprocal function.