Trisectrix of Maclaurin

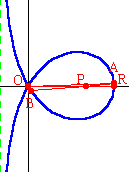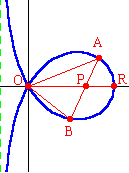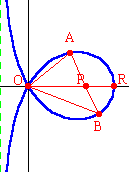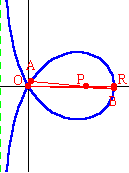The curve pictured to the left is given by the equation: $x^3+xy^2+ay^2-3ax^2=0$. Point $O$ is the node of the curve, located at the origin. Point $R$ is the other point of intersection with the $x$-axis. The distance $OR$ is $3a$ units. Point $P$ is located along the $x$-axis such that the distance $OP$ is $2a$ units.

Using only Euclidean tools (a compass and a straightedge), the trisection of an angle is an impossibility. But if one adds another tool in the form of a plane curve, then trisection may become a possibility. The Trisectrix of Maclaurin is one of those curves which make angle trisections possible.

To trisect an angle, place a copy of the angle in such a way that the vertex is at point $P$, and one side of the angle lies along the positive $x$-axis. Then the other side of the angle will intersect the loop of the trisectrix at point $A$ above the $x$-axis (or point $B$ below the $x$-axis). In other words, the original angle is $\angle AOR$ (or $\angle BOR$). Draw line segment $OA$ (or $OB$). Then $\angle AOR=\dfrac13\angle APR$ and $\angle BOR=\dfrac13\angle BPR$.

Colin Maclaurin (1698-1746) became a professor of mathematics at the University of Aberdeen in 1717, and at the University of Edinburgh in 1725. Among his many areas of study were higher plane curves.