
We use MathJax
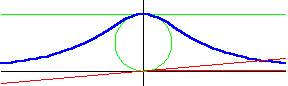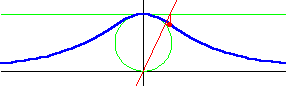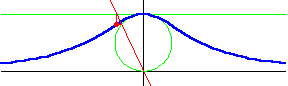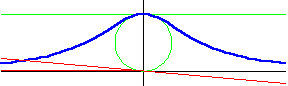
In the graph above, a green circle of radius $a$ is centered at $(0,a)$, and a green horizontal line is $2a$ units above the $x$-axis, tangent to the circle. The red line drawn through the origin will intersect both the circle (at a point other than the origin) and the horizontal line. Using the $x$-coordinate from the intersection with the horizontal line, and the $y$-coordinate from the intersection with the circle, the blue curve given by the equation $x^2y=4a^2(2a-y)$ is generated.
Maria Gaetana Agnesi (1718-1799) of Milan received her early education through tutors provided by her father, and later through self-study and personal contacts. Drawn toward mathematics, she compiled much of the mathematics then known in her most important work, Instituzioni Analitiche, in 1748. Her achievement brought her an appointment to the University of Bologna, although she never filled the position. Included in her work was a discussion of a curve called la versiera, or twisted curve, earlier studied by Pierre de Fermat (1601-1665) and by Guido Grandi (1671-1742). Agnesi's work was eventually translated into English, and at that time the term la versiera was corrupted into l'aversiera, or witch. So the English translator referred to the curve as the Witch of Agnesi.