Estimating Population Parameters

We have studied ways to describe data, and the relationship between samples and populations. What happens if we do not know anything about a population? can we determine the parameters of a population based only on information gleaned from a sample?

Estimators

Suppose $\theta$ is a population parameter, and we want to estimate it from a sample. If the sample size is $n$, then the sample parameter $\hat{\theta}$ will be a function of the random variables $X_1$, $X_2$, ... $X_n$. The randomness in the data will also make the sample parameter $\hat{\theta}$ a random variable, and therefore susceptible to sampling error.

To have a good estimator, we would like four qualities to be present.

The estimator should be unbiased, meaning that the expected value of the estimator should be equal to the population parameter. In other words, $E(\hat{\theta}) = \theta$.
The estimator should be efficient, meaning that the standard error of the estimator is relatively small, compared to other possible estimators.
The estimator should be robust, meaning that it is both unbiased and efficient for many different population distributions.
The estimator should be consistent, meaning that the estimator's value approaches the population parameter as the sample size increases without bound. In other words, for any $\epsilon > 0$, we have $\lim\limits_{n \to \infty} P(|\hat{\theta} - \theta| < \epsilon) = 1$.

Two Unbiased Estimators

Since we proved earlier (see Sums of Random Variables) that $E(\bar{X}) = E(X)$, the sample mean $\bar{x}$ is an unbiased estimator of the population mean $\mu$. It is also a consistent estimator, and on a normal distribution it is an efficient estimator, although on a heavy-tailed distribution a trimmed mean may be more efficient.

Interestingly, the population formula for a variance, when performed on a sample, is a biased estimator of the population variance. One way of recognizing this is that when sampling from a normal population, it would be quite rare to get a value well into the long tails of that distribution, and therefore the variance computed from the population formula would underestimate the true variance. Adjusting the variance formula to divide by $n-1$ rather than $n$ corrects this bias. Therefore, the sample variance, $s^2$, has a different formula than the population variance, $\sigma^2$. And $s^2$ is an unbiased estimator of $\sigma^2$.

The proof of the unbiased character of $s^2$ proceeds as follows. First, we note that

\begin{align} \sum \limits_{i=1}^n (X_i - \bar{X})^2 &= \sum \limits_{i=1}^n (X_i - \mu + \mu - \bar{X})^2 \\ &= \sum \limits_{i=1}^n (X_i - \mu)^2 + 2(\mu - \bar{X}) \sum \limits_{i=1}^n (X_i - \mu) + \sum \limits_{i=1}^n (\mu - \bar{X})^2 \\ &= \sum \limits_{i=1}^n (X_i - \mu)^2 + 2(\mu - \bar{X}) n( \bar{X} - \mu) + n (\mu - \bar{X})^2 \\ &= \sum \limits_{i=1}^n (X_i - \mu)^2 - n (\bar{X} - \mu)^2 \end{align}

Then, recalling that $Var(X) = E((X - \mu)^2)$ by definition (see Moments and Moment Generating Functions), and that $Var(\bar{X}) = \dfrac{Var(X)}{n}$, (see Sums of Random Variables), we have:

\begin{align} E(S^2) &= E \left( \dfrac{1}{n-1} \sum \limits_{i=1}^n (X_i - \bar{X})^2 \right) \\ &= \dfrac{1}{n-1} \left( E \left( \sum \limits_{i=1}^n (X_i - \mu)^2 - n (\bar{X} - \mu)^2 \right) \right) \\ &= \dfrac{1}{n-1} \sum \limits_{i=1}^n E((X_i - \mu)^2) - \dfrac{n}{n-1} E((\bar{X} - \mu)^2) \\ &= \dfrac{1}{n-1} \sum \limits_{i=1}^n Var(X) - \dfrac{n}{n-1} Var(\bar{X}) \\ &= \dfrac{n}{n-1} \sigma^2 - \dfrac{n}{n-1} \dfrac{\sigma^2}{n} \\ &= \sigma^2 \end{align}

Point Estimates and Interval Estimates

The sample statistics $\bar{x}$ and $s$ are called point estimates of the population parameters $\mu$ and $\sigma$, in that they provide a single value for each parameter. Yet reporting point estimates will almost guarantee that the reported values will be wrong, due to sampling error.

But we know the sampling distributions of our parameters. Therefore, we can give intervals, rather than points, to describe the possible values of each parameter, with some known probability that our assertions are correct. That known probability is called the confidence level of our estimate, and is denoted by the quantity $1 - \alpha$. The variable $\alpha$ is called the significance level, and in the context of an interval estimate describes the probability that sampling error has given an incorrect result.

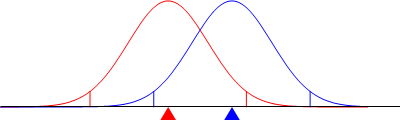
Let us focus for now on the sample mean as an estimate of the population mean. For sufficiently large sample sizes, the sample means will be normally distributed about the population mean. In the graph below, the red triangle indicates a population mean, and the red normal curve shows a sample mean distribution about the population mean. Also indicated are two short red vertical lines, between which we find 95% of the area under that curve. Now our sample mean will rarely fall at exactly the population mean, but is more likely to be somewhat different, as indicated by the blue triangle below. When we assume that the sample mean is our best estimate of the population mean, we are assuming the blue normal curve is the distribution of sample means. Of course, the curve is incorrect, but we see that if the blue sample mean is within the 95% interval about the population mean, then the red population mean is within a 95% interval about the sample mean. Therefore, we can use the sample mean distribution about a sample mean (rather than about the unknown population mean) to generate probabilities that our estimate is correct.

Graph of two identical
distributions, one about the population mean and one about the sample mean