
We use MathJax
One of the major processes in statistical inference is to determine how likely a claim is, or whether a particular result is statistically significant. Both of these questions are answered through a hypothesis test.
A hypothesis test in statistics is like a proof in mathematics, or an essay in English composition. It is an explanation of a situation, not just an answer. Although the result of the hypothesis test is itself interesting (just as the conclusion of a mathematical theorem, or the main point of an essay), the "answer" is not the focus of the process. Rather, we are interested in the argument that proves the result.
There are actually two main approaches to doing a hypothesis test. In our discussion, we shall focus on the approach most commonly used in today's technological era, the p-value approach. For our comments about the other approach, often called the classical approach (which finds critical values), see the section "Differences in the Classical Approach" below.
In order to discuss the structure of a hypothesis test, it helps to have an example. So we begin with an example, after which we provide the discussion of the argument presented in the example.
A certain brand of dog food comes in 10-pound bags (or so the bag claims). A sample of 100 bags has a mean weight of 9.90 pounds, with a standard deviation of 0.30 pounds. Is the mean weight of the dog food bags really 10 pounds?
There are six parts to the hypothesis test, as seen above. Those six parts always come in the following order:
Each of these six parts must be present in a complete hypothesis test done by the p-value approach.
Mathematically, there are six possible hypotheses, corresponding to the six possible relations between two quantities: $=, \ne, >, \ge, <, \le$. The claim to be tested will use one of these relations. Also, these six relations come in three opposite pairs, and each of those pairs leads to a type of hypothesis test: two-tailed, left-tailed, or right-tailed. The left-tailed and right-tailed tests are often referred to as one-tailed tests. The graphs for the three types of tests make this distinction more visually (although their interpretation depends on whether the p-value or critical value approach is used). The following chart sorts out the details.
| $H_0$: Null Hypothesis | same, equal $=$ |
at least, $\ge$ but use $=$ |
at most, $\le$ but use $=$ |
| $H_a$: Alternative Hypothesis | different $\ne$ |
less than $<$ |
more than $>$ |
| Type of Test | two-tailed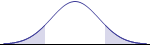 |
left-tailed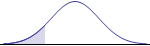 |
right-tailed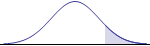 |
Identifying the logical relation in the original claim, together with its mathematical opposite, automatically selects a type of test. The original claim may be equivalent to the null hypothesis relation, or to the alternative hypothesis relation. But the null hypothesis must always contain the equality condition ($=, \ge, \le$), while the alternative hypothesis does not. In our example above, the question "Is the mean weight ... really 10 pounds?" led us to using the two-tailed test, with its "equal" or "not equal" pair, and the null hypothesis had to contain the equality condition.
Now it is common practice to always write the null hypothesis as an equality, even though the original claim may have been an inequality. That is because the mathematics requires a specific claim to be tested, not a range of claims. In other words, in the one-tailed tests, a tension exists between the mathematical needs and the logical situation, which a few statisticians find objectionable. However, most statisticians accept the validity of one-tailed tests, and we shall also.
In writing the hypothesis, the relation must be between two quantities. Most often, the first quantity is an unknown population parameter (such as $\mu$, $\sigma$, or $p$), and the second quantity is the numerical value of the claim. In our example above, the hypotheses were about population means, and whether the mean weight of the bags of dog food was 10 pounds or not. Those two options were written symbolically in our hypotheses.
Notationally, some statisticians will use the symbol $H_1$, rather than $H_a$, to indicate the alternative hypothesis.
The choice of a level of significance is a decision as to when a particular value from a random sample would be considered highly unlikely, assuming that the null hypothesis was true. The symbol for the level of significance is $\alpha$, and the most common value for $\alpha$ is 5%. This was our choice, and so our example includes $\alpha = 0.05$. Other common choices are 10% and 1%.
Now samples involve randomness, and the distribution of sample means (or other parameters) is well known. It is quite possible to obtain a sample whose values are quite unlike the original population, but for larger sample sizes, it is not very likely. The choice of the level of significance also implies what percentage of the truly random samples we would actually ascribe to something other than randomness (and thereby incorrectly reject the null hypothesis). Since we do not want to make frequent errors on this point, we tend to choose $\alpha$ to be fairly small. With a level of 5%, then only one out of every 20 random samples will be incorrectly identified as due to something other than randomness. That is, we are giving the benefit of the doubt to the null hypothesis 19 out of 20 times, or 95% of the time.
So when should you use a different level of significance? When the cost of a particular type of error is more than can be tolerated. If that cost should involve human life, a much smaller $\alpha$ may be warranted. However, the error in a decision situation can be of two types. This will be discussed later. But quite often, a textbook problem will specify the level of significance to be used.
This description of the level of significance ought to seem quite similar to the discussion of the confidence level of a confidence interval. In fact, they are very related. The confidence level is given by $1 - \alpha$, the level of significance is given by $\alpha$, and they are the same $\alpha$. The major difference is that the "interval" in the hypothesis test need not be centered on the parameter being sought. Instead, the hypothesis test "interval" could be an interval to infinity.
The test statistic is the function of the unknown parameter for which the probability distribution is known. If we were to test a population mean when we already knew the population standard deviation (a rather unlikely scenario in practice, but useful for learning the ideas), then the test statistic would be the z-score for the sample mean, whose distribution (for large enough sample sizes) is approximately normal. Most often, we test population means without knowing the population standard deviation, in which case the sample means are distributed (for large enough sample sizes) according to the t-distribution. A test statistic for proportions is based on the normal distribution. A test statistic for variances and standard deviations is based on the chi-square distribution. Other test statistics exist for other situations.
In our example above, the population standard deviation was unknown, so we substituted the sample value in its place. Since our sample size was much larger than 30, that meant that the sample means of the population would be distributed according to the t-distribution, and we used the test statistic $t = \dfrac{\bar{x} - \mu_0}{s/\sqrt{n}}$. We substituted our values into that formula, and obtained a numerical result.
The p-value gives the probability that a random sample from the population claimed by the null hypothesis would have produced a more unlikely test statistic value than the one actually obtained. For a one-tailed test, we use the distribution implied by the test statistic, and find the area under the curve beyond that value. For a two-tailed test, we do the same thing, but we double the answer.
The graphs corresponding to the type of test above can be used to help determine and interpret the p-value. In this approach, the test statistic occurs at the boundary between the shaded and unshaded region of the graph. (For a two-tailed test, there are two boundaries, and the value of the second boundary is the numerical opposite of the first boundary.) Therefore, the shaded region(s) are the pictoral representation of the p-value.
In our example above, the distribution for our test statistic was the t-distribution, with $n-1$ degrees of freedom. So we found the area under the t-curve having 99 degrees of freedom, to the left of our test statistic of $t=-3.33$, and then doubled that area for our two-tailed test.
At this point, we have all the information needed to make a conclusion. Under the assumption that the null hypothesis is true, the p-value is examined to see how unusual our sample was. If our p-value was less than the level of significance $\alpha$, we deem our sample to be very unusual, and therefore reject the null hypothesis. If the p-value was greater than or equal to $\alpha$, then we give the benefit of the doubt to the null hypothesis, and our conclusion would be either "Accept $H_0$" or "Fail to reject $H_0$". The implications behind this latter choice are discussed in the section on Errors below.
However, a statistical conclusion is by itself insufficient. It needs to be rephrased in the context of the original question. This is required for two reasons. First, the original claim may or may not have been equivalent to the null hypothesis, and so the contextual conclusion will clarify the result. Secondly, if you need to report your statistical result to management, you cannot assume that your audience will understand the statistical lingo. (If they did, they probably would not have hired you.) So each conclusion must be stated in terms that the man on the street would understand. There are essentially three possible conclusions.
The parenthetical comment "(the ... hypothesis in words)" is always replaced by words appropriate to the context of the original problem. The other parenthetical comment provided in the rejection scenario is sometimes included to make our situation more explicit, although it is not really necessary. If a hypothesis test makes a conclusion, it is generally assumed that it was done so on the basis of evidence. (But see the section on Errors with regard to the conclusion of accepting $H_0$.)
Five of the six steps from the p-value approach also exist in the classical approach. The main difference is that instead of computing a p-value, the classical approach finds critical values. The critical values are the scores which separate the rejection regions from the non-rejection regions, using the numerical scale of the distribution of the test statistic.
For the classical approach, the graphs corresponding to the type of test also direct our process and interpretation. The level of significance is the area of the shaded region, and is called the rejection region. If a two-tailed test is done, that sum of the areas of the rejection region is the level of significance. An inverse distribution function on the value $\alpha$ (or for two-tailed tests, on the value $\alpha/2$) is used to obtain the critical value(s).
Critical values are always determined immediately after the level of significance, and before the test statistic. This order of steps is to help ensure the integrity of the statistical process, so that one is not determining what makes a significant result after the result is found.
In our example above, if we had computed critical values, they would have been values of $t_{\alpha/2}$ for 99 degrees of freedom. Since $\alpha = 0.05$, then $\alpha/2 = 0.025$, and $t_{\alpha/2} = -1.984$. And since we are doing a two-tailed test, there are actually two critical values, $\pm 1.984$. (If you do not have access to an inverse t-distribution program, then when $n \ge 30$, the normal distribution is often used as an approximation to the t-distribution. The critical values based on the normal distribution would have been $\pm 1.96$.)
After both the critical value(s) and the test statistic are obtained, the classical approach then makes a conclusion. If the test statistic falls in the rejection region (beyond the critical value), then the null hypothesis is rejected. If the test statistic falls in the non-rejection region, then the null hypothesis is not rejected. In our example, the test statistic $t = -3.33$ fell well beyond the critical values $\pm 1.984$, and therefore we would reject the null hypothesis (as we did before).
The classical approach and the p-value approach will always yield the same conclusion. The differences are primarily a matter of style of presentation, not in the mathematical results. Some would also argue that the p-value approach is easier, which is true only if access to the necessary inverse distribution function is not available.