
We use MathJax
Conditional probabilities provide a way to measure uncertainty when partial knowledge is assumed. Sometimes, we would like to reverse the roles of the partial knowledge and the unknown event. That is, if $A$ and $B$ are two events, and we already know $P(A|B)$, there are times when we would like to know $P(B|A)$. To do this, we use Bayes Theorem. A simplified version of the formula is:
| $P(B|A) = \dfrac{P(B) \cdot P(A|B)}{P(B) \cdot P(A|B) + P(\overline{B}) \cdot P(A|\overline{B})}$ |
Frankly, it is much easier to set up a tree diagram to obtain the required probabilities, and that is how we intend to approach all such problems. When doing this, we simply need to recognize that the formula is equivalent to $P(B|A) = \dfrac{P(A \cap B)}{P(A)}$. That is, the formula is just a rewritten form of the Conditional Rule for probability.
Suppose 0.1% of the American population currently has lung cancer, that 90% of all lung cancer cases are smokers, and that 21% of those without lung cancer also smoke. (These values are fairly close to the values given on the American Lung Association web site as of 2011.) Consider the following questions.
We begin by recognizing two variables for each subject, smoking and lung cancer. Let event $S$ be the smokers, and event $L$ be those with lung cancer. The data given specifies $P(L)=0.001$, $P(S|L)=0.90$, and $P(S|\overline{L})=0.21$. The questions are asking $P(L|S)$ and $P(L|\overline{S})$. Since the conditional probabilities in the information and the question are reversed, we recognize the need to use a Bayes Theorem approach. Therefore, we shall construct a tree diagram, with the lung cancer data in the first set of branches to take advantage of the given information.
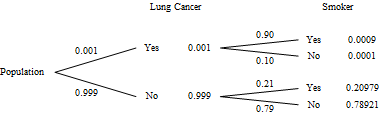
After including the original data, we recognize that the probabilities on each set of branches must add to one, and the probabilities along branches must multiply to the final result. With the completed tree diagram, we can answer the questions.
This analysis does not say that smoking caused lung cancer. The only way statistics can be used to determine causation is for the researcher to control the variables involved. To do this, the researcher would have to randomly assign some subjects to be smokers, and some to not smoke, and then determine the incidence of lung cancer among his participants. However, controlling the lives of human subjects in this way would not be acceptable.
One prominent manufacturer of medical tests offers a test for chlamydia (a sexually transmitted disease) that has a sensitivity of 76.4% and a specificity of 93.2%. In other words, the test correctly identifies 76.4% of individuals tested who have the disease by giving a positive result, and correctly identifies 93.2% of the individuals who are healthy by giving a negative result. Currently, it is estimated that 1.5% of the American population has chlamydia. If one individual is randomly selected from the population and tests positive for chlamydia, what is the probability that he/she does not have the disease?
Our variables are the presence of chlamydia and the test result. Let $C$ be those who have chlamydia, and let $T$ be those who have a positive test result. The data states that $P(C)=0.015$, $P(T|C)=0.764$, and $P(\overline{T}|\overline{C})=0.932$. The question being asked is the value of $P(\overline{C}|T)$. Once again, we construct a tree diagram.

We then have $P(\overline{C}|T) = \dfrac{P(\overline{C} \cap T)}{P(T)} = \dfrac{0.06698}{0.01146+0.06698} = 0.8539$. In other words, there is an 85% chance that a positive result would be a false positive. This is a horrendous result. You might think that if the sensitivity of the test was higher, the situation would be rectified. However, the real problem is the rarity of the condition in the general population. Such medical tests should not be done unless there is some reason to suspect the disease, and if a positive result occurs, a second (different) test might be appropriate to confirm the diagnosis of the first test.
A game show host offers the contestant the chance to win a car hidden behind one of three doors, simply by choosing the correct door. The contestant makes his choice. Then the host, who knows where the car is, opens one of the other doors that does not reveal the car. At this point, there are two doors, one of which has the car, and the host offers the contestant the opportunity to switch doors. Should the contestant switch?
Monty Hall was the game show host on the TV show "Let's Make a Deal", where contestants were offered a very similar opportunity. The problem was discussed in The American Statistician magazine in 1975, and again by columnist Marilyn vos Savant in Parade magazine in 1990. It has become known as the Monty Hall problem. Many people are fascinated by it, and many people come to the wrong conclusion.
At first glance, we might argue as follows: The car had an equally likely chance of being behind any of the three doors. Once the host opened a door, there were only two doors left, which meant the sample space now only had two equally-likely items, each with probability $\dfrac12$. Therefore, there would be no reason to switch doors. But this analysis is wrong!
Let us analyze the situation more carefully. Since the location of the car is unknown, we shall let $A$, $B$, and $C$ be the events that the car is behind doors $A$, $B$, and $C$ respectively. The door the contestant originally chose is very well known, he announced it to all concerned. Let us suppose the contestant chose door $A$. (The same analysis could be done by assuming he chose door $B$, or door $C$, and would result in the same answer.) Now the host must open a door that does not contain the car, and he also will not open the door chosen by the contestant. If the contestant has chosen correctly, the host then has a choice of doors to open, and we assume that he will make his choice in a random fashion. Let $H_B$ and $H_C$ be the events that the host opens door $B$ and $C$, respectively. That leads us to the following tree diagram.
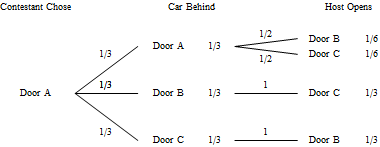
Notice that the probabilities associated with the door opened by the host are equal. That is, $P(H_B) = \dfrac16+\dfrac13=\dfrac12$ and $P(H_C) = \dfrac16+\dfrac13=\dfrac12$. By itself, there is no clue where the car is based only on the door that the host opened.
But the probabilities we want to know are those that are conditioned on the door that the host opened. There are four such probabilities.
We notice that whichever door the host opened, the probability that the car is behind door $A$ (the contestant's choice) remains $\dfrac13$, while the probability that the car is behind the other door is $\dfrac23$. In other words, the act of revealing a door did not maintain the equality of the doors, but in fact maintained the probability of the contestant's original choice. Under these circumstances, the contestant should always switch.
If this seems counterintuitive, consider a slight modification to the problem. Suppose there were a thousand doors, and only one car. The contestant chooses a door, but has a probability of only $0.001$ of choosing the correct door. Now the host opens 998 doors, revealing that the car was not behind one of those 998 doors. There are two doors left. Should you really continue to maintain that the contestant's original choice was correct?