Randomized Response

Surveying people is an excellent way to gather data about the thoughts or actions of a population on an issue. However, if the question being studied is sensitive, involving illegality, immorality, or some other characteristic that the community would frown upon, it can be difficult to get respondents to answer truthfully. Using a randomized response technique will allow the respondent to answer truthfully without the questioner knowing what question the respondent is answering, yet at the same time not losing information about the population proportion in question. Once again, a tree diagram will help sort out the situation.

A Question and its Complement

Suppose a researcher wants to collect data on methamphetamine use. Since drug use is a sensitive subject, the researcher prepares a set of 100 cards, as follows:

58 cards say "I DO use meth at least once this past week."
42 cards say "I DO NOT use meth at least once this past week."

The researcher shows the interviewees the cards, so that they see there are two different statements in roughly equal quantities. Then the cards are shuffled, the subject chooses one card, either agrees or disagrees with the statement on the card, then returns the card to the deck. In this way, the researcher has no idea whether the subject was agreeing (or disagreeing) to meth use or not. After interviewing 1200 people, the researcher found 513 agreed with the statement on their card. Assuming everyone answered truthfully, what percentage of the subjects used meth at least once this past week?

The two independent variables here are the type of card and the use of methamphetamines. (The answer that the subject provides is not an independent variable, since it can be determined from the values of the other two variables.) Let $D$ be the event of receiving an "I DO" card, and let $U$ be the event of meth use. From the cards provided, we have $P(D) = \dfrac{58}{100} = 0.58$ and $P(\overline{D})= \dfrac{42}{100} = 0.42$. We also have $\dfrac{513}{1200}=0.4275$ as the proportion who agreed with their card. The event of agreeing is a combination of the two events, $D \cap U$ and $\overline{D} \cap \overline{U}$.

In order to use a tree diagram, we need to identify the probabilities that are conditional on the card received. In other words, we need $P(U|D)$, $P(\overline{U}|D)$, $P(U|\overline{D})$, and $P(\overline{U}|\overline{D})$. We don't have that data. But since the cards were shuffled, we can assume that users and non-users received the "I DO" cards in the same proportion. In other words, we can assume that events $U$ and $D$ are statistically independent. Therefore, let $x=P(U)$ be the proportion of meth users that we want to find. Then independence says $x = P(U|D) = P(U|\overline{D})$ as well. So we can now complete our tree diagram.

We now have a way to find the value of $x$. The probabilities for those who agreed with their card are $P(D \cap U) = 0.58x$ and $P(\overline{D} \cap \overline{U}) = 0.42(1-x)$. This gives the equation $0.58x + 0.42(1-x) = 0.4275$. Solving, we find $x=P(U) = 0.046875$. In other words, about 4.7% of the sample used meth this past week.

For any individual interview, the researcher will not know what question was being answered. Yet there are still a couple of potential difficulties. Both questions are still sensitive, and if the person being interviewed is at all suspicious, he might still be unwilling to answer truthfully. Also, when a user is presented an "I DO NOT" card, we are asking them to respond with a double negative, which has different interpretations in different languages.

A Harmless Question

Let's consider a redesigned study. Rather than a researcher preparing cards with a statement and its complement, only one sensitive question will be asked. ("Did you use meth at least once this past week?) But before the subject answers, he is instructed to flip a coin out of the sight of the researcher, and proceed as follows.

If the coin comes up heads, answer the question truthfully.
If the coin comes up tails, answer "yes".

After interviewing 800 people, the researcher found 414 answered "yes". Assuming everyone answered truthfully, what percentage of the subjects used meth at least once this past week?

Now our two independent variables are the result of the coin flip, and the use of meth. (The answer to the question is not an independent variable, as it can be determined from the values of the other two variables.) Let $H$ be the event that the coin flip results in a head, and let $U$ be the event of meth use. Assuming a fair coin, we have $P(H)=0.5$ and $P(\overline{H})=0.5$. We also have $\dfrac{414}{800} = 0.5175$ who answered "yes". Let $x=P(U)$. We now have the following tree diagram.

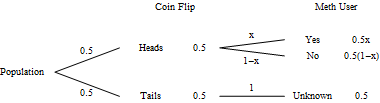
The individuals who answered "yes" are a combination of the two events $H \cap U$ and $\overline{H}$. This gives the equation $0.5x + 0.5 = 0.5175$. Solving, we find $x=P(U)=0.035$. In other words, 3.5% of the sample used meth this past week.

Compared to the first approach (where a question and its complement were used), this approach simplifies the process greatly. It avoids the double negative that occurs with the use of the complementary question. One of the two cases clearly contains no information about meth use, and therefore the suspicions of the subject would be lessened. And yes, even the algebra is (slightly) simpler.