Sample Mean Distributions

We have considered many different population distributions. We could take a sample from each of these distributions, and consider the distribution of sample means. The main implication of the Central Limit Theorem is that for any population distribution, for a sufficiently large sample, the distribution of sample means will be approximately normal. This result suggests that there is an interplay between the population and its samples, which we will begin investigating through an example.

Samples of a Population

Suppose that a biologist discovers two individuals of a new species of snake. He measures their lengths (among other characteristics) in order to provide information about this new species.

But before we focus on the biologist's findings, let us take a more omniscient view. Let us suppose that we know all about the population, even though the biologist does not. Unknown to him, the world population of this species of snake consists of exactly five individuals, whose lengths (in feet) are given by the values ${2,4,6,8,10}$. Some basic computations will reveal the following population parameters: $N = 5$, $\mu = 6$, $\sigma^2 = 8$, and $\sigma = \sqrt{8} \approx 2.83$. Furthermore, a graph will quickly confirm that the population is most similar to a uniform distribution.

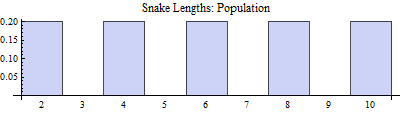
Graph of the distribution of the population of snakes

Simple probability questions can be asked about this population. For example, the probability that a randomly selected snake is between 4.5 and 7.5 feet long, by counting the relevant entries in the distribution, is $P(4.5 < x < 7.5) = \dfrac15 = 0.2$.

Now we know that the biologist found exactly two individuals. So let us consider all possible samples of size $n = 2$. From a counting argument, we know that there are precisely ${}_5 C_2 = 10$ possible samples, so it is a fairly easy task to write them all down. As we do so, we will also give the sample mean, $\bar{x}$, for each sample, since that is the measurement that the biologist would be reporting.

Sample	2, 4	2, 6	2, 8	2, 10	4, 6	4, 8	4, 10	6, 8	6, 10	8, 10
Sample Mean	3	4	5	6	5	6	7	7	8	9

Although there were 10 possible samples, we note that there were only 7 possible values for the sample mean. Some of the values could occur in more than one way. So if the two snakes that the biologist found were from a random sample, so that each sample would be equally likely to be found as any other, then some possible values of the sample mean are more likely than others. In other words, even though the population distribution was uniform, the distribution of sample means is not uniform. Let us display the probability distribution of the random variable $\bar{X}$, which is also called the sampling distribution of the mean.

$\bar{x}$	$P(\bar{X} = \bar{x})$
3	0.1
4	0.1
5	0.2
6	0.2
7	0.2
8	0.1
9	0.1

Because we have considered every possible sample, this distribution is a population of sample means. And we can determine the parameters of this population also. With some basic computations, we find: : $N_{\bar{x}} = 10$, $\mu_{\bar{x}} = 6$, $\sigma^2_{\bar{x}} = 3$, and $\sigma_{\bar{x}} = \sqrt{3} \approx 1.73$. The distribution is still symmetric, but it is not uniform.

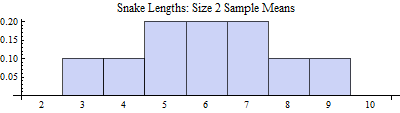
Graph of the distribution of the sample means of snakes

We can also ask simple probability questions about this distribution. The probability that a pair of randomly selected snakes has a mean length of between 4.5 and 7.5 feet long, by adding appropriate values from the PDF of the sample means, is

$P(4.5 < \bar{x} < 7.5) = P(x=5) + P(x=6) + P(x=7) = 0.2 + 0.2 + 0.2 = 0.6$

Interestingly, and quite significantly, we see that it is much more likely for the sample mean to be between 4.5 and 7.5 feet than it is for a single individual to have that length.

Now the biologist only found one of those samples. Let us suppose he found the two largest individuals, having lengths 8 feet and 10 feet. In that case, he would report the following sample statistics: $n=2$, $\bar{x} = 9$, $s^2 = 2$, and $s = \sqrt{2} \approx 1.41$. Obviously, by reporting these values, the biologist is not accurately representing the population of snakes. This is not his fault, but is due to sampling error, which occurs whenever the characteristics of the sample do not match the population characteristics. Of course, that means sampling error almost always occurs. Yet the probability of having a very poor sample tends to be quite small, as long as the samples are random and sufficiently large.

Summarizing the Results

Looking back at the example, we see that there were measurements at three different levels, the population, the sample, and the population of sample means. Notationally, we defined these quantities as:

Population: size $N = N_x$, mean $\mu = \mu_x$, and standard deviation $\sigma = \sigma_x$
Sample: size $n$, mean $\bar{x}$, and standard deviation $s$
Population of sample means: size $N_{\bar{x}}$, mean $\mu_{\bar{x}}$, and standard deviation $\sigma_{\bar{x}}$

The following three results describe the connection between the population and the distribution of sample means.

The mean of the sample means obeys the formula $\mu_{\bar{x}} = \mu$.
The standard deviation of the sample means obeys the formula $\sigma_{\bar{x}} = \dfrac{\sigma}{\sqrt{n}} \sqrt{ \dfrac{N - n}{N - 1}}$. The quantity $\sqrt{ \dfrac{N - n}{N - 1}}$ is called the finite population correction factor, and it can be ignored whenever the population size $N$ is infinite or very large (at least 20 times the sample size).
If the sample size $n$ is large enough (but still finite), then the Central Limit Theorem says that the samples means will be approximately normally distributed. A sample size of $n \ge 30$ is sufficiently large for any distribution, but if the original population is normal, then any sample size is enough (that is, $n \ge 1$).

Some Examples

Suppose the random variable $X$ has a continuous uniform distribution on the interval $[0,20]$. What is the probability that a random sample of 30 values will have a sample mean between 8 and 12?

Being uniform, the original population has a mean of $\mu = 10$, and a standard deviation of $\sigma = \sqrt{ \dfrac{(20-0)^2}{12}} \approx 5.774$.
Since a continuous distribution represents an infinite population, the standard deviation of sample means of size 30 will be $\sigma_{\bar{x}} = \dfrac{\sigma}{\sqrt{n}} \approx \dfrac{5.774}{\sqrt{30}} \approx 1.054$.
Since $n \ge 30$, the sample means will be approximately normally distributed, so we then compute z-scores for the values 8 and 12. We find $z = \dfrac{8 - 10}{1.054} \approx -1.897$ and $z = \dfrac{12 - 10}{1.054} \approx 1.897$.
Then $P(8 < \bar{x} < 12) = P(-1.897 < z < 1.897) = \Phi(1.897) - \Phi(-1.897) = \operatorname{normalcdf} (-1.897,1.897) \approx 0.9422$. (Of course, this is much more likely than the 20% probability of finding a single value in that interval.

Suppose the mean household income in the USA is $\$51,344$, with a standard deviation of $\$15,377$. What is the probability that a random sample of 124 households will have a mean household income of more than $\$54,000$?

For any distribution, when the sample size is at least 30, the sample means will be approximately normal, with a standard error of $\sigma_{\bar{x}} = \dfrac{\sigma}{\sqrt{n}} = \dfrac{15377}{\sqrt{124}} \approx 1380.90$. The finite population correction factor was not necessary, because the number of households in the USA is far greater than the sample size.
Computing the z-score, we obtain: $z = \dfrac{54000 - 51344}{1380.90} \approx 1.92$.
Then $P(\bar{x} > 54000) = P(z > 1.92) = 1 - \Phi(1.92) = \operatorname{normalcdf}(1.92,\infty) \approx 0.0274$.