The Definition(s) of Trigonometry

Many trigonometry textbooks offer several different "definitions" of the trig functions. This is not really a good practice from a logical point of view. Each mathematical object ought to have only one definition, so that no inconsistencies can result. We shall choose the unit circle approach for our definition, as it allows values to take on any real number, and provides a unique definition for the trig function of that angle. The other "definitions" will be introduced as theorems.

Unit Circle Definition

If $(x,y)$ is any point on the unit circle, and $t$ is the directed distance from $(1,0)$ to $(x,y)$, measured counterclockwise along the circumference of the unit circle, then the six trig functions are defined as follows:

$\sin t=y$	$\tan t=\dfrac{y}{x}$	$\sec t=\dfrac{1}{x}$
$\cos t=x$	$\cot t=\dfrac{x}{y}$	$\csc t=\dfrac{1}{y}$

In other words, the point $(x,y)$ is equal to $(\cos t, \sin t)$.

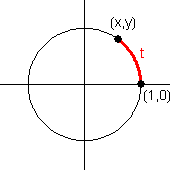
Other "definitions" are actually results that can be derived from the unit circle definition.

Standard Position Ratios Theorem

If $t$ is an angle in standard position, the point $(x,y)$ is any point on the terminal side of $t$ other than the origin, and $r$ is the distance from the origin to the point, then the following identities are true:

$\sin t=\dfrac{y}{r}$	$\tan t=\dfrac{y}{x}$	$\sec t=\dfrac{r}{x}$
$\cos t=\dfrac{x}{r}$	$\cot t=\dfrac{x}{y}$	$\csc t=\dfrac{1}{y}$

The proof involves similar triangles, and the assumption that angle $t$ is equivalent to the arc length $t$ along the unit circle.

Proof: Let $P$ be the point $(x,y)$, $O$ be the origin, and point $Q$ have coordinates $(x,0)$. Let $A$ be the intersection of the unit circle with the line $OP$. Draw a line through $A$ parallel to $PQ$, and let $B$ be the intersection of this line with $OQ$.

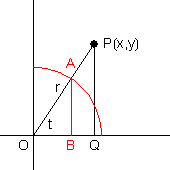
Then $OAB$ and $OPQ$ are similar triangles, which implies $\dfrac{OP}{PQ}=\dfrac{OA}{AB}$. But $PQ=y$, $OP=r$, $AB=\sin t$, and $OA=1$, therefore $\sin t=\dfrac{y}{r}$. The standard position ratios for the other trig functions can be found similarly.♦

It is true that the Standard Position Ratios Theorem can be used as a definition, and the Unit Circle results produced as a theorem. However, the Standard Position Ratios approach involves an arbitrary parameter $r$, and so it becomes necessary to show that unique results are produced. The Unit Circle Definition produces unique results on its own.

Triangle Ratios Theorem

If $ABC$ is a triangle with $C=90^\circ$, and standard nomenclature is used (i.e. angle $A$ is opposite side $a$, etc.), then the following identities are true:

$\sin A=\dfrac{a}{c}$	$\tan A=\dfrac{a}{b}$	$\sec A=\dfrac{c}{b}$
$\cos A=\dfrac{b}{c}$	$\cot A=\dfrac{b}{a}$	$\csc A=\dfrac{c}{a}$

Proof: We shall impose a pair of coordinate axes on triangle $ABC$. Let point $A$ be the origin. Use segment $AC$ as the direction of the positive $x$-axis. Locate the $y$-axis perpendicular to the $x$-axis through the origin, so that the positive $y$-direction and point $B$ are on the same side of $AC$. The triangle ratios follow from the coordinates of point $B$ and the Standard Position Ratios Theorem.♦

<>Sometimes, a trigonometry textbook will use the triangle ratios as the definition of the trigonometric functions. One weakness of this approach is that angles of right triangles are always between 0 and 90 degrees, so trig functions of other angles are yet undefined.

A very different approach was taken by Edmund Landau in 1934. In his calculus textbook, he defined the sine function as the sum of a power series:

\begin{equation*} \sin x=\sum_{m=0}^\infty \dfrac{(-1)^m}{(2m+1)!} x^{2m+1} \end{equation*} From this definition, and a similar definition for the cosine function, he derived all of the trigonometric results. In other words, the trigonometric functions can be defined only in terms of infinite sums of polynomials, without any prior reference to triangles.