Generating the Sine Function

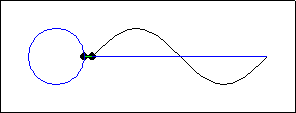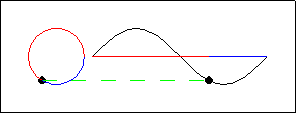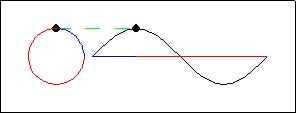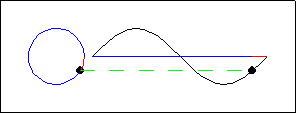
Graph of a circle and sine wave, with 2 points, one on each graph, moving in coordinated fashion.

This animation consists of a sine wave function on a horizontal axis, and a unit circle to the left. Two points, one on each figure, travel in coordinated fashion. Assume that the "origin" of the coordinate system is located at the left end of the horizontal axis. Several connections between the circle and the sine function are depicted.

The circumference of the circle equals the period of the sine wave, which is the length of the horizontal axis in this figure.
The $x$-coordinate of the point on the sine wave equals a length of arc on the unit circle. That is, the horizontal distance travelled by the point on the sine wave (shown in either blue or red) equals the distance travelled by the point on the unit circle (shown in the same color).
The two points have the same $y$-coordinate. This is illustrated by the horizontal dashed green line.

These connections can be summarized by describing the motion in terms of a "wrapping function". In mathematics, a function is a rule that, to each input, assigns at most one output. As input, the wrapping function uses a number (describing the length of arc from the rightmost point of the unit circle). Output consists of the point on the unit circle obtained by "wrapping" that length around the circle. In function notation, the wrapping function can be described by:

\begin{equation*} W(t) = (\cos t ,\sin t) \end{equation*}

The corresponding point on the sine wave is given (in a slightly different coordinate system) by the function:

\begin{equation*} y(t) = \sin t \end{equation*}

A cosine function can be obtained in a similar fashion, if the circle is wrapped clockwise beginning at its upper $y$-intercept, the point $(0,1)$.