Multiples of 15 Degrees

Trigonometry texts always include material early in the course on finding the exact values of trig functions of the angles $0^\circ, 30^\circ, 45^\circ, 60^\circ$, and $90^\circ$. It is also true that by a similar argument, exact values of trig functions of the angles $15^\circ$ and $75^\circ$ may also be found. These angles are equivalent to unit circle arc lengths that are multiples of $\dfrac{\pi}{12}$.

Trig Values of Multiples of $\dfrac{\pi}{12}$

$\theta$	$\sin\theta$	$\cos\theta$	$\tan\theta$	$\cot\theta$	$\sec\theta$	$\csc\theta$
$\dfrac{\pi}{12}$	$\dfrac{\sqrt{6}-\sqrt{2}}{4}$	$\dfrac{\sqrt{6}+\sqrt{2}}{4}$	$2-\sqrt{3}$	$2+\sqrt{3}$	$\sqrt{6}-\sqrt{2}$	$\sqrt{6}+\sqrt{2}$
$\dfrac{5\pi}{12}$	$\dfrac{\sqrt{6}+\sqrt{2}}{4}$	$\dfrac{\sqrt{6}-\sqrt{2}}{4}$	$2+\sqrt{3}$	$2-\sqrt{3}$	$\sqrt{6}+\sqrt{2}$	$\sqrt{6}-\sqrt{2}$

Proof: Using the angle difference identity for sine, we have:

\begin{align} \sin\dfrac{\pi}{12} &= \sin\left(\dfrac{\pi}{4}-\dfrac{\pi}{6}\right) = \sin\dfrac{\pi}{4}\cos\dfrac{\pi}{6}-\cos\dfrac{\pi}{4}\sin\dfrac{\pi}{6} \\ &= \dfrac{\sqrt{2}}{2} \cdot\dfrac{\sqrt{3}}{2}-\dfrac{\sqrt{2}}{2}\cdot\dfrac12 = \dfrac{\sqrt{6}-\sqrt{2}}{4} \end{align}

The derivation of the other values is similar.♦

If a half-angle formula is used, then the result $\sin\dfrac{\pi}{12}=\dfrac{\sqrt{2-\sqrt{3}}}{2}$ would be obtained. But these two results are identical, since $\left(\dfrac{\sqrt{6}-\sqrt{2}}{4}\right)^2 = \dfrac{6-2\sqrt{12}+2}{16}=\dfrac{2-\sqrt{3}}{4}=\left(\dfrac{\sqrt{2-\sqrt{3}}}{2}\right)^2$.

Alternative Proof: Let triangle $TPU$ be inscribed in rectangle $PQRS$, so that angle $PTU$ is 90 degrees, angle $QPT$ is 30 degrees, angle $TPU$ is 45 degrees, and segment $PU$ has length 1. Then angle $UPS$ is 15 degrees, and angle $RTU$ is 30 degrees.

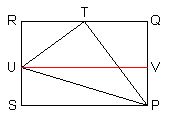
By the Triangle Ratios Theorem, we have:

\begin{align} \sin 15^\circ &= US = PQ-RU = PT\cos 30^\circ - TU \sin 30^\circ \\ &= \cos 45^\circ \cos 30^\circ - \sin 45^\circ \sin 30^\circ = \dfrac{\sqrt{2}}{2}\cdot\dfrac{\sqrt{3}}{2}-\dfrac{\sqrt{2}}{2}\cdot\dfrac12\ = \dfrac{\sqrt{6}-\sqrt{2}}{4} \end{align}

The derivation of the other values is similar.♦