
We use MathJax
Trigonometry texts always include material early in the course on finding the exact values of trig functions of the angles $0^\circ, 30^\circ, 45^\circ, 60^\circ$, and $90^\circ$. It is also true that by a similar argument, exact values of trig functions of the angles $18^\circ, 36^\circ, 54^\circ$, and $72^\circ$ may also be found. These angles are equivalent to unit circle arc lengths that are multiples of $\dfrac{\pi}{10}$.
| $\theta$ | $\sin\theta$ | $\cos\theta$ | $\tan\theta$ | $\cot\theta$ | $\sec\theta$ | $\csc\theta$ |
| $\dfrac{\pi}{10}$ | $\dfrac{\sqrt{5}-1}{4}$ | $\dfrac{\sqrt{10+2\sqrt{5}}}{4}$ | $\dfrac{\sqrt{25-10\sqrt{5}}}{5}$ | $\sqrt{5+2\sqrt{5}}$ | $\dfrac{\sqrt{50-10\sqrt{5}}}{5}$ | $\sqrt{5}+1$ |
| $\dfrac{\pi}{5}$ | $\dfrac{\sqrt{10-2\sqrt{5}}}{4}$ | $\dfrac{1+\sqrt{5}}{4}$ | $\sqrt{5-2\sqrt{5}}$ | $\dfrac{\sqrt{25+10\sqrt{5}}}{5}$ | $\sqrt{5}-1$ | $\dfrac{\sqrt{50+10\sqrt{5}}}{5}$ |
| $\dfrac{3\pi}{10}$ | $\dfrac{1+\sqrt{5}}{4}$ | $\dfrac{\sqrt{10-2\sqrt{5}}}{4}$ | $\dfrac{\sqrt{25+10\sqrt{5}}}{5}$ | $\sqrt{5-2\sqrt{5}}$ | $\dfrac{\sqrt{50+10\sqrt{5}}}{5}$ | $\sqrt{5}-1$ |
| $\dfrac{2\pi}{5}$ | $\dfrac{\sqrt{10+2\sqrt{5}}}{4}$ | $\dfrac{\sqrt{5}-1}{4}$ | $\sqrt{5+2\sqrt{5}}$ | $\dfrac{\sqrt{25-10\sqrt{5}}}{5}$ | $\sqrt{5}+1$ | $\dfrac{\sqrt{50-10\sqrt{5}}}{5}$ |
Proof: Let $A$ be the point $(1,0)$ on the unit circle, and choose points $B$, $C$, $D$, and $E$ on the unit circle counterclockwise from $A$ so that arc lengths $AB$, $BC$, $CD$, $DE$, and $EA$ are each $\dfrac{2\pi}{5}$. Let $(x,y)$ be the coordinates of point $B$, and let $(v,w)$ be the coordinates of point $C$. Then, by symmetry, the coordinates of point $D$ are $(v,-w)$, and the coordinates of point $E$ are $(x,-y)$. Since all of these points are on the unit circle, the equations $x^2+y^2=1$ and $v^2+w^2=1$ are both true.
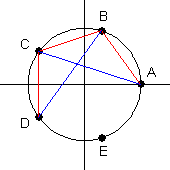
Since the line segments $AB$ and $BC$ are equal, we apply the distance formula to obtain the equation $(x-1)^2+y^2=(x-v)^2+(y-w)^2$, which simplifies to $yw=x-xv$. Similarly, the equality of the line segments $AC$ and $BD$ will produce an equation which simplifies to $yw=xv-v$. Equating these results gives $v=\dfrac{x}{2x-1}$. The equality of the line segments $AB$ and $CD$ will produce an equation which simplifies to $4w^2=2-2x$. Using $v^2+w^2=1$ to substitute for the variable $w$, then using $v=\dfrac{x}{2x-1}$ to substitute for the variable $v$, then removing fractions, we obtain the polynomial equation $8x^3-4x^2-6x+2=0$. Since 1 is a solution of this equation, the polynomial factors into a linear and a quadratic expression. Since point $B$ is in the first quadrant, the value of $x$ must be positive, and the quadratic formula produces $x=\dfrac{-1+\sqrt{5}}{4}$. The values of the variables $y$, $v$, and $w$ then can be produced by substitution.
The values of the sine and cosine functions are then related to the variables through symmetry arguments as follows:
\begin{align} x &= \sin\dfrac{\pi}{10}=\cos\dfrac{2\pi}{5} \qquad\qquad v=-\cos\dfrac{\pi}{5}=-\sin\dfrac{3\pi}{10} \\ y &= \cos\dfrac{\pi}{10}=\sin\dfrac{2\pi}{5} \qquad\qquad w=\sin\dfrac{\pi}{5}=\cos\dfrac{3\pi}{10} \end{align}The values of the other four trigonometric functions can be found with the ratio and reciprocal identities.♦
Alternate Proof: Suppose triangle $ABC$ is isosceles, with congruent sides $AB$ and $AC$ each of length 1, and the measure of angle $BAC$ is $36^\circ$. Then angles $ABC$ and $ACB$ are also congruent, and since the sum of the angles of a triangle is $180^\circ$, the measure of each of these two angles is $72^\circ$.
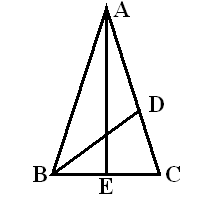
Now bisect angle $ABC$, and let point $D$ be the intersection of side $AC$ with the bisector of angle $ABC$. Now angle $ABD$ is $36^\circ$, so triangle $ABD$ is isosceles, with congruent sides $AD$ and $BD$. Also, since angle $DBC$ is $36^\circ$ and angle $BCD$ is $72^\circ$, we find that angle $BDC$ must be $72^\circ$, therefore triangle $BDC$ is isosceles with congruent sides $BD$ and $BC$. Note that triangles $ABC$ and $BCD$ are similar triangles, by AAA Similarity.
Let $x$ be the length of side $BC$ (which is also the length of $BD$ and of $AD$). Then by similar triangles, we obtain the proportion $\dfrac{AB}{BC}=\dfrac{BC}{CD}$, which is equivalent to $\dfrac{1}{x}=\dfrac{x}{1-x}$. Solving this equation by cross-multiplying, using the quadratic formula and discarding the negative solution, we obtain $x=\dfrac{\sqrt{5}-1}{2}$.
Now bisect angle $BAC$, and let point $E$ be the intersection of side $BC$ with the bisector of angle $BAC$. Since triangle $ABC$ is isosceles, triangles $ABE$ and $ACE$ are congruent, and by corresponding parts $CE$ is half the measure of $BC$, and angle $AEC$ is a right angle.
Triangle $ACE$ is now observed to be a right triangle whose acute angles measure $18^\circ$ and $72^\circ$, and with sides of lengths $AC = 1$ and $CE=\dfrac{\sqrt{5}-1}{4}$. By the definitions of sine and cosine, we have $\sin 18^\circ =\cos 72^\circ =\dfrac{\sqrt{5}-1}{4}$. All other results can be obtained through the use of sum, difference, and double angle formulas, and the Pythagorean identity.♦