
We use MathJax
The graphs of the trigonometric functions, and values at many different arc lengths can be determined. The statements and proofs could also be described in terms of angles. However, since our original definition involved arc lengths, we retain the arc length interpretation here, thus also demonstrating that the trigonometric values do not actually depend on triangles.
The graphs of the trig functions are most easily understood through the idea of projections. The sine function can be described as the horizontal projection of the point onto the $y$-axis, and the cosine function as the vertical projection of the point onto the $x$-axis. The tangent and cotangent functions are the projections from the origin onto the lines $x=1$ and $y=1$, respectively. The secant and cosecant functions are the projections of the point along the tangent line of the circle at that point onto the $x$-axis and $y$-axis, respectively.
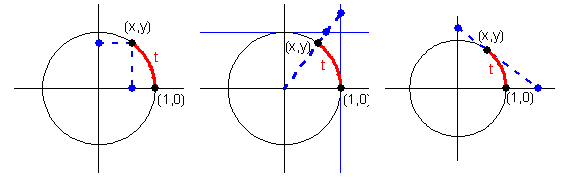
These projections give rise to the following function graphs, domains, and ranges.
| Function: | $f(x)=\sin x$ | $f(x)=\tan x$ | $f(x)=\sec x$ |
| Domain: | $(-\infty,\infty)$ | $\bigcup\limits_{k=-\infty}^\infty \left(\left(k-\dfrac12\right)\pi, \left(k+\dfrac12\right)\pi\right)$ | $\bigcup\limits_{k=-\infty}^\infty \left(\left(k-\dfrac12\right)\pi, \left(k+\dfrac12\right)\pi\right)$ |
| Range: | $[-1,1]$ | $(-\infty,\infty)$ | $(-\infty,-1]\cup[1,\infty)$ |
| Graph: | 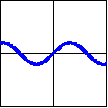 |
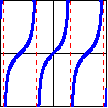 |
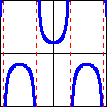 |
| Function: | $f(x)=\cos x$ | $f(x)=\cot x$ | $f(x)=\csc x$ |
| Domain: | $(-\infty,\infty)$ | $\bigcup\limits_{k=-\infty}^\infty \left(k\pi,(k+1)\pi \right)$ | $\bigcup\limits_{k=-\infty}^\infty \left(k\pi,(k+1)\pi \right)$ |
| Range: | $[-1,1]$ | $(-\infty,\infty)$ | $(-\infty,-1]\cup[1,\infty)$ |
| Graph: | 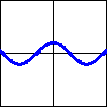 |
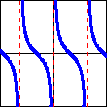 |
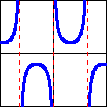 |
Using the Cofunction Theorem, it can be confirmed that the graphs of the cosine, cotangent, and cosecant are simple transformations of the first three graphs.