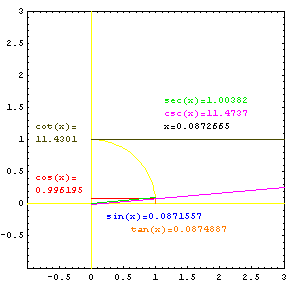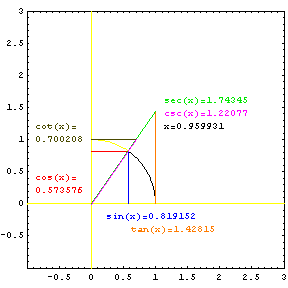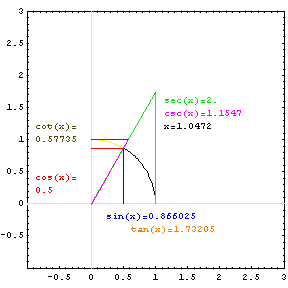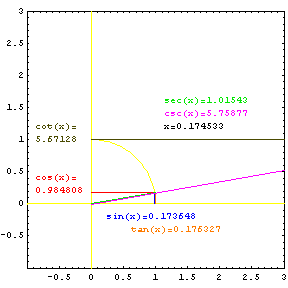Each of the six trig functions can be thought of as a length related to the unit circle.

The sine and cosine functions are distances from the unit circle to the axes.

The tangent and cotangent functions are the lengths of lines tangent to the unit circle from the axis to the ray sweeping out the angle.

The secant and cosecant functions are lengths of the ray, or secant line, from the origin to its intersection with the tangent lines.