Angle Sum and Difference Identities

Trigonometric functions of the sum or difference of two angles occur frequently in applications. There are several ways of confirming these results.

Angle Sum and Difference Theorem

The following identities are true for all values for which they are defined:

$\sin(A\pm B) = \sin A \cos B \pm \cos A \sin B$

$\cos(A\pm B) = \cos A \cos B \mp \sin A \sin B$

$\tan(A\pm B) = \dfrac{\tan A \pm \tan B}{1 \mp \tan A \tan B}$

$\cot(A\pm B) = \dfrac{\cot A \cot B \mp 1}{\cot B \pm \cot A}$

$\sec(A\pm B) = \dfrac{\sec A \sec B \csc A \csc B}{\csc A \csc B \mp \sec A \sec B}$

$\csc(A\pm B) = \dfrac{\sec A \sec B \csc A \csc B}{\sec A \csc B \pm \csc A \sec B}$

Proof: Let $P$ be the point with coordinates $(1,0)$. Measured counterclockwise from point $P$, let $Q$ be the point whose arc length is $A$, let $R$ be the point whose arc length is $A+B$, and let $S$ be the point whose arc length is $-B$. Then $(\cos A,\sin A)$ are the coordinates of point $Q$, $(\cos(A+B),\sin(A+B))$ are the coordinates of point $R$, and $(\cos(-B),\sin(-B))$ are the coordinates of point $S$.

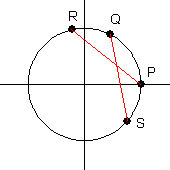
Note that the lengths of segments $PR$ and $QS$ are equal. Using the distance formula, we get:

\begin{equation*} (\cos(A+B)-1)^2+(\sin(A+B)-0)^2=(\cos A-\cos(-B))^2+(\sin A-\sin(-B))^2 \end{equation*}

Through the use of the symmetric and Pythagorean identities, this simplifies to become the angle sum formula for the cosine.

The proof of the angle difference formula for the cosine proceeds as follows:

\begin{align} \cos(A-B) &= \cos(A+(-B)) \\ &= \cos A \cos(-B)-\sin A \sin(-B) \\ &= \cos A \cos B + \sin A \sin B \end{align}

Then by using the cofunction theorem, we can obtain the formulas for the sine:

\begin{align} \sin(A \pm B) &= \cos\left( \dfrac{\pi}{2}-(A\pm B)\right) \\ &= \cos\left( \left(\dfrac{\pi}{2}-A\right) \mp B\right) \\ &= \cos\left(\dfrac{\pi}{2}-A\right)\cos B \pm \sin\left(\dfrac{\pi}{2}-A\right)\sin B \\ &= \sin A \cos B \pm \cos A \sin B \end{align}

With the results of the sine and cosine formulas, the other four formulas can be derived.♦

The formulas can also be derived using triangles. Although we refer to the following derivation as a proof, in fact the values of angles $A$ and $B$ allowed by the derivation are quite limited, and a more general proof is actually required.

Alternate Proof: Let positive angles $A$ and $B$ be given, whose sum is less than 90 degrees. Construct segment $PU$ with length 1. Construct triangle $TPU$ so that angle $TPU$ is equal to angle $A$, and angle $TUP$ is equal to the complement of $A$. Construct the circumscribed rectangle $PQRS$ so that angle $QPT$ is equal to angle $B$, angle $QPU$ is equal to the sum of angles $A$ and $B$, point $T$ is on segment $QR$ and $U$ is on segment $RS$. Note that angle $RTU$ is also equal to angle $B$.

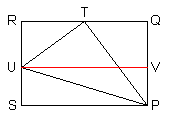
By the Triangle Ratios Theorem, we have:

\begin{align} \sin(A+B) &= UV \\ &= RT+QT \\ &= TU \cos B + PT \sin B \\ &= \sin A \cos B + \cos A \sin B \end{align}

The proof of the angle sum identity for the cosine is similar. The angle difference identities can be derived directly from the same figure by identifying angle $A$ with angle $TPS$, and angle $B$ with angle $TPU$.♦

There are several classes of identities which are immediate corollaries of the Angle Sum and Difference Theorem.

Double Angle Theorem

The following identities are true for all values for which they are defined:

$\sin 2t = 2 \sin t \cos t$	$\cos 2t = \cos^2 t - \sin^2 t$
$\tan 2t = \dfrac{2 \tan t}{1-\tan^2 t}$	$\cot 2t = \dfrac{\cot^2 t - 1}{2 \cot t}$
$\sec 2t = \dfrac{\sec^2 t \quad\csc^2 t}{\csc^2 t - \sec^2 t}$	$\csc 2t = \dfrac{\sec t \csc t}{2}$

Proof: The proof of the double angle formula for sine proceeds as follows:

\begin{align} \sin 2t &= \sin (t+t) \\ &= \sin t \cos t + \cos t \sin t \\ &= 2 \sin t \cos t \end{align}

The proofs of the double angle formulas for the other five functions are similar.♦

Power-Reducing Theorem

The following identities are true for all values for which they are defined:

$\sin^2 t = \dfrac{1-\cos 2t}{2}$	$\cos^2 t = \dfrac{1+\cos 2t}{2}$
$\tan^2 t = \dfrac{1-\cos 2t}{1+\cos 2t}$	$\cot^2 t = \dfrac{1+\cos 2t}{1-\cos 2t}$
$\sec^2 t = \dfrac{2}{1+\cos 2t}$	$\csc^2 t = \dfrac{2}{1-\cos 2t}$

Proof: To find the power-reducing formula for the sine, we start with the cosine double angle formula and replace the cosine squared term using the Pythagorean identity. The resulting equation can be solved for the sine squared term. The proofs of the power-reducing formulas for the other five functions are similar.♦

Half-Angle Theorem

The following identities are true for all values for which they are defined:

$\sin\dfrac{t}{2} = \pm\sqrt{\dfrac{1-\cos t}{2}}$	$\cos\dfrac{t}{2} = \pm\sqrt{\dfrac{1+\cos t}{2}}$
$\tan\dfrac{t}{2} = \dfrac{1-\cos t}{\sin t}$	$\cot\dfrac{t}{2} = \dfrac{\sin t}{1+\cos t}$
$\sec\dfrac{t}{2} = \pm\sqrt{\dfrac{2 \sec t}{\sec t+1}}$	$\csc\dfrac{t}{2} = \pm\sqrt{\dfrac{2 \sec t}{\sec t-1}}$

Proof: The half-angle formulas for sine and cosine are found immediately from the power-reducing formulas by substitution and square root. The half-angle formulas for secant and cosecant proceed similarly, including a reciprocal identity as the last step. For the tangent half-angle formula, we first note the following:

\begin{align} \dfrac{1-\cos 2t}{\sin 2t} &= \dfrac{(\sin^2 t+\cos^2 t)-(\cos^2 t-\sin^2 t)}{2\sin t\cos t} \\ &= \dfrac{2\sin^2 t}{2\sin t\cos t} = \dfrac{\sin t}{\cos t} = \tan t \end{align}

Substitution into this result produces the tangent half-angle formula. The proof of the cotangent formula is similar.♦

Product-to-Sum Theorem

The following identities are true for all real values.

$\sin A\sin B=\dfrac12 [(\cos(A-B)-\cos(A+B)]$

$\sin A\cos B=\dfrac12 [(\sin(A+B)+\sin(A-B)]$

$\cos A\cos B=\dfrac12 [(\cos(A+B)+\cos(A-B)]$

Proof: Expanding and simplifying the right hand side of each formula using the Angle Sum and Difference Theorem will produce the left hand side.♦

Sum-to-Product Theorem

The following identities are true for all real values.

$\sin A\pm\sin B=2\sin\dfrac{A\pm B}{2}\cos\dfrac{A\mp B}{2}$

$\cos A+\cos B=2\cos\dfrac{A+B}{2}\cos\dfrac{A-B}{2}$

$\cos A-\cos B=-2\sin\dfrac{A+B}{2}\sin\dfrac{A-B}{2}$

Proof: By substituting $\dfrac{A\pm B}{2}$ for the variables in the Product-to-Sum formulas, these formulas can be derived.♦