
We use MathJax
In this section, we consider several identities applicable to triangles.
If $ABC$ is a triangle (where $a$ is the side opposite angle $A$, etc.), then the following identity holds:
| $\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}$ |
Proof: In triangle $ABC$, drop an altitude from point $C$ to side $AB$ (extending $AB$ if necessary). Let point $D$ be the intersection of the altitude with side $AB$, and let $h$ be the length of $CD$.
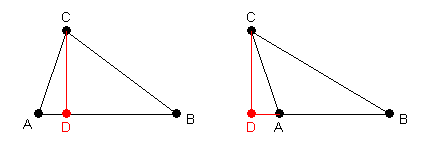
Considering triangles $ACD$ and $BCD$, we have $b\sin A=h=a\sin B$, from which one proportion follows. (If angle $A$ is obtuse, then we actually have $h=b\sin(180^\circ-A)=b\sin A$, and the proportion still follows.) Dropping an altitude from a second vertex will provide a second proportion and prove the theorem.♦
Alternate Proof: Triangle $ABC$ can be circumscribed by a circle. Let $O$ be the center of the circle, and construct segments $OA$ and $OB$ (each having length equal to the radius $r$ of the circle). Let $P$ be the midpoint of segment $AB$, and construct segment $OP$.
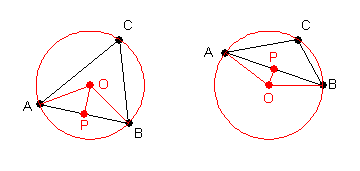
Since triangle $OAB$ is isosceles, triangles $OPA$ and $OPB$ are congruent right triangles. By the Inscribed Angle Theorem of geometry, angle $ACB$ is half the measure of angle $AOB$.
Now, if angle $ACB$ is acute, then angle $ACB$ is congruent to angle $AOP$, and we have:
\begin{equation*} \dfrac{c}{\sin C}=\dfrac{c}{\sin AOP}=\dfrac{c\cdot AO}{AP}=\dfrac{cr}{c/2}=2r \end{equation*}If angle $ACB$ is obtuse, then angle $AOB$ is the external angle, and we have:
\begin{equation*} \dfrac{c}{\sin C}=\dfrac{c}{\sin (180^\circ-AOP)}=\dfrac{c}{\sin AOP}=\dfrac{c\cdot AO}{AP}=\dfrac{cr}{c/2}=2r \end{equation*}If angle $ACB$ is a right angle, then side $c$ is the diameter, and the same result still holds. The other ratios can be handled similarly, with the same result. Thus, the theorem is proved (with the additional information that the ratio is the diameter of the circumscribed circle).♦
If $ABC$ is a triangle (where $a$ is the side opposite angle $A$), then the following identity holds:
| $a^2=b^2+c^2-2bc\cos A$ |
Proof: We begin with the same pictures as used in the first proof of the Law of Sines. Let $h$ be the length of $CD$, and $x$ be the length of $AD$. Then $h=b\sin A$ and $x=\pm b\cos A$, where the sign depends on whether angle $A$ is acute or obtuse. By the Pythagorean Theorem, we have:
\begin{align} a^2 &= (c\mp x)^2+h^2 \\ &= c^2 \mp 2cx + x^2 +h^2 \\ &= c^2 \mp 2c(\pm b\cos A)+b^2\cos^2 A+b^2 \sin^2 A \\ &= b^2 + c^2 - 2bc \cos A \end{align}If $ABC$ is a triangle (where $a$ is the side opposite angle $A$, etc.), then the following identity holds:
| $\dfrac{a+b}{a-b}=\dfrac{\tan\dfrac{A+B}{2}}{\tan\dfrac{A-B}{2}}$ |
Proof: By the Law of Sines, $\dfrac{a}{\sin A}=\dfrac{b}{\sin B}$ implies $b\sin A-a\sin B=0$. Therefore, we have:
\begin{align} b\sin A-a\sin B &= -(b\sin A-a\sin B) \\ a\sin A+b\sin A-a\sin B-b\sin B &= a\sin A+a\sin B-b\sin A-b\sin B \\ (a+b)(\sin A-\sin B) &= (a-b)(\sin A+\sin B) \\ 2(a+b)\sin\dfrac{A-B}{2}\cos\dfrac{A+B}{2} &= 2(a-b)\sin\dfrac{A+B}{2}\cos\dfrac{A-B}{2} \\ (a+b)\tan\dfrac{A-B}{2} &= (a-b)\tan\dfrac{A+B}{2} \\ \dfrac{a+b}{a-b} &= \dfrac{\tan\dfrac{A+B}{2}}{\tan\dfrac{A-B}{2}} \end{align}If $ABC$ is a triangle (but not a right triangle), then the following identity holds:
| $\tan A+\tan B+\tan C=\tan A \tan B \tan C$ |
Proof: The identity can be verified by use of the angle sum and difference formulas for the tangent.
\begin{align} \tan A+\tan B+\tan C &= \tan A+\tan B+\tan(180^\circ-(A+B)) \\ &= \tan A+\tan B+\dfrac{\tan 180^\circ -\tan(A+B)}{1+\tan 180^\circ \tan(A+B)} \\ &= \tan A+\tan B-\tan(A+B) \\ &= \tan A+\tan B-\dfrac{\tan A+\tan B}{1-\tan A \tan B} \\ &= \dfrac{-(\tan A \tan B)(\tan A+\tan B)}{1-\tan A \tan B} \\ &= \tan A \tan B (-\tan (A+B)) \\ &= \tan A \tan B \tan(180^\circ -(A+B)) \\ &= \tan A \tan B \tan C \end{align}