
We use MathJax
Typically, we define an inverse function with the statement
From this statement, it immediately follows that the domain of $f$ is the range of $f^{-1}$, and the range of $f$ is the domain of $f^{-1}$.
However, this assumes that the original function is a one-to-one function (that is, for each $y$-value of the function, there exists only one $x$-value which produces that $y$-value). This assumption is certainly not true for the trigonometric functions, or even for any periodic function. Therefore, in order to achieve an inverse which is a function, we must restrict the original function to some subset of its original domain on which it will be one-to-one. Many such subsets are possible, and for three of the trigonometric functions, there is general agreement on which subset to choose.
The inverse trig functions are often called "arc functions", since given a value of a trig function, they produce the length of arc needed to obtain that value. For example, the inverse sine function can be written as either $\sin^{-1}x$ or as $\arcsin x$. We shall use the latter notation.
| Function: | $y=\arcsin x$ | $y=\arccos x$ | $y=\arctan x$ |
| Defined by: | $x=\sin y$ | $x=\cos y$ | $x=\tan y$ |
| Domain: | $[-1,1]$ | $[-1,1]$ | $(-\infty,\infty)$ |
| Range: | $\left[ -\dfrac{\pi}{2},\dfrac{\pi}{2}\right]$ | $[0,\pi]$ | $\left( -\dfrac{\pi}{2},\dfrac{\pi}{2}\right)$ |
| Graph: | 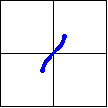 |
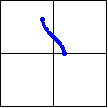 |
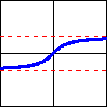 |
For the other three inverse trig functions, there is not complete agreement on the subset to which the original function should be restricted. Therefore, we will give the two most common approaches, labeling them with subscripts so that the properties of both definitions can be studied.
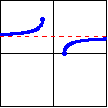
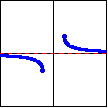
| Function: | $y=\operatorname{ arccot}_1 x$ | $y=\operatorname{ arcsec}_1 x$ | $y=\operatorname{ arccsc}_1 x$ |
| Defined by: | $x=\cot y$ | $x=\sec y$ | $x=\csc y$ |
| Domain: | $(-\infty,\infty)$ | $(-\infty,-1]\cup[1,\infty)$ | $(-\infty,-1]\cup[1,\infty)$ |
| Range: | $(0,\pi)$ | $\left[0,\dfrac{\pi}{2}\right) \cup \left(\dfrac{\pi}{2},\pi\right]$ | $\left[-\dfrac{\pi}{2},0\right) \cup \left(0,\dfrac{\pi}{2}\right]$ |
| Graph: | 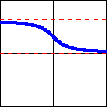 |
 |
 |
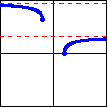
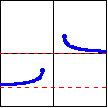
| Function: | $y=\operatorname{ arccot}_2 x$ | $y=\operatorname{ arcsec}_2 x$ | $y=\operatorname{ arccsc}_2 x$ |
| Defined by: | $x=\cot y$ | $x=\sec y$ | $x=\csc y$ |
| Domain: | $(-\infty,\infty)$ | $(-\infty,-1]\cup[1,\infty)$ | $(-\infty,-1]\cup[1,\infty)$ |
| Range: | $\left(-\dfrac{\pi}{2},0\right) \cup \left(0,\dfrac{\pi}{2}\right]$ | $\left[0,\dfrac{\pi}{2}\right) \cup \left[\pi,\dfrac{3\pi}{2}\right)$ | $\left(-\pi,-\dfrac{\pi}{2}\right] \cup \left(0,\dfrac{\pi}{2}\right]$ |
| Graph: | 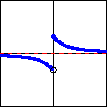 |
 |
 |