Sums of Geometric Sequences

The terms of a geometric sequence can also be added to find their sum. When a geometric sequence has an unbounded long-term behavior, we will be restricted to adding a finite number of terms. However, sometimes the terms of a geometric sequence will approach zero, and in that case, an sum of an infinite number of terms can be found.

Numerical Results for a Partial Sum

Consider the sum $5+15+45+135+\ldots+2657205$. We quickly notice that the terms have a common ratio of 3, so this is the sum of a geometric sequence whose explicit formula is $a_n=5(3^{n-1})$. Solving the equation $5(3^{n-1})=2657205$, we find that 2657205 is the thirteenth term of the sequence.

We can also use some ingenuity to sum this geometric sequence, as follows.

\begin{align} & \phantom. 3s= \phantom{-5-}15+45+135+405+\ldots+7971615 \\ & \underline{-s=-5-15-45-135-\ldots-2657205} \\ & \phantom. 2s = -5 \phantom{+15+45+135+405+\ldots} + 7971615 \\ & \phantom2 s= \frac{7971615-5}{2}=3985805 \end{align}

In a very similar fashion, it can be shown that every geometric sequence has the $n$th partial sum $s_n=\dfrac{a_1(1-r^n)}{1-r}$.

We can also use the properties of sums, as follows.

\begin{equation*} \sum_{k=1}^{13} 5(3^{k-1}) = \frac{5}{3} \sum_{k=1}^{13} 3^k = \frac{5}{3} \left(\frac{3^{13+1}-3}{3-1}\right) = 3985805 \end{equation*}

A Specific Partial Sum Formula

Once again, either approach can be used to create a formula for the sequence of partial sums $s_n=\sum\limits_{k=1}^n 5(3^{k-1})$.

$s_n=\dfrac{5(1-3^n)}{1-3}=\dfrac{5}{2}(3^n-1)$
$\sum\limits_{k=1}^n 5(3^{k-1})=\dfrac{5}{3}\sum\limits_{k=1}^n 3^k = \dfrac{5}{3} \left(\dfrac{3^{n+1}-3}{3-1}\right) = \dfrac{5}{2}(3^n-1)$

Partial Sum Applications

The geometric sequence is also used in a variety of applications. Examples include:

Tim's starting salary is $\$24,000$ per year, and he receives a $5\%$ cost of living raise each year. The explicit formula is $a_n=24000(1.05^{n-1})$, his salary in the tenth year is $a_{10}=24000(1.05^{10-1})=37231.88$, and he earned a total of $s_{10}=\dfrac{24000(1-1.05)^{10}}{1-1.05}=301869.42$ during that ten-year period.
Kelly deposited $\$300$ in her account at the end of each month for twenty years, and the bank is paying her $6\%$ interest compounded monthly. The amounts generated by each deposit form a geometric sequence with explicit formula $a_n=300(1.005^{n-1})$, where the first deposit is actually the 240th term, and the last deposit is the first term of the sequence. The balance in the account after twenty years will be the sum of the amounts generated by each deposit, which is $s_n=\dfrac{300(1-1.005^{240})}{1-1.005} = 138612.27$.

Sum of an Infinite Geometric Sequence

When a sequence is geometric, and its common ratio is in the interval $-1 < r < 1$, then the sum of the infinite geometric sequence (called a geometric series) may be found. Since . $\lim\limits_{n\to\infty} r^n = 0$ when $-1 < r < 1$, , we then have $\lim\limits_{n\to\infty} s_n = \lim\limits_{n\to\infty} \dfrac{a_1 (1-r^n)}{1-r} = \dfrac{a_1}{1-r}$. In other words, the sum of an infinite geometric sequence is given by $s_{\infty} = \dfrac{a_1}{1-r}$, when $-1 < r < 1$.

Consider, for example, the sum $\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\dfrac{1}{16}+\dfrac{1}{32}+\ldots$. The explicit formula of this sequence is $a_n=\left(\dfrac12\right)^n$, and we see that it is a geometric sequence whose first term and ratio are both $\dfrac12$. The sum of this sequence is therefore $s_{\infty}=\dfrac{\frac12}{1-\frac12}=1$. This sum is also illustrated in the areas of the rectangles in the following diagram.

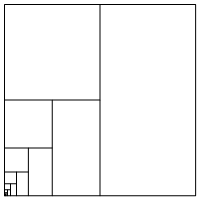
a square box being bisected ad infinitum

Some people would object to the sum being equal to exactly 1, but rather want to say that it approaches the value 1. Philosophically, this is the position that infinities cannot actually be achieved, but are only potential and can only be approached. If the sum is stopped early and only a finite number of terms are added, then the partial sum will be short of the value 1. And in fact, the partial sums are approaching the value 1. But with a series, we are taking the position that we have achieved the infinite aspect of this problem, and that all infinite number of terms are added, and in this case, the value is exactly equal to 1.

Application Using a Series

As an application, consider a ball that is dropped from a height of 15 feet, and rebounds to 75% of its previous height on each bounce. The geometric series with first term 15 and ratio 0.75 has sum $s_{\infty}=\dfrac{15}{1-0.75}=60$. The ball travels this distance in each direction (up and down), except on the first leg where it only travels down. Therefore, the total distance traveled is twice the sum minus 15 feet, or a total of 105 feet.