Imaginary Numbers and Trigonometry

In our earlier discussion of imaginary numbers, we learned how a picture of the complex number $2+3i$ can be drawn.

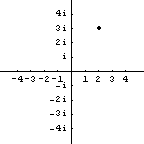
a rectangular coordinate graph with a point at 2, 3

If we draw a right triangle in the picture, then we have:

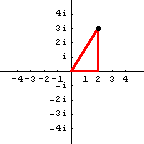
a right triangle with vertices at the origin, at x equals 2, and at the complex number 2 plus 3 i

The parts of the complex number $2+3i$ are shown by the horizontal and vertical sides of the triangle. The hypotenuse of the right triangle has length $\sqrt{13}$, found by using the Pythagorean Theorem or the distance formula.

In the triangle, if we use $P$ for the name of the angle at the origin, then we can rewrite the number $2+3i$ by using its trigonometric components. The horizontal component is $\sqrt{13}\cos P$, the vertical component is $\sqrt{13}(\sin P)i$, so the number $2+3i$ is the same as $\sqrt{13}(\cos P + i \sin P)$. Basically, every complex number can be written in the form

\begin{equation*} a+bi= r (\cos P + i \sin P) \end{equation*}

Multiplying and dividing

There are many identities in trigonometry, and they are the key to multiplying and dividing complex numbers. Suppose we have the two complex numbers $r (\cos P + i \sin P)$ and $s (\cos Q + i \sin Q)$. When we multiply them using distributive property, we obtain $rs (\cos P \cos Q + i \cos P \sin Q + i \sin P \cos Q - \sin P \sin Q)$. But the formulas for the sine and cosine of a sum allow us to rewrite this result as

\begin{equation*} [r (\cos P + i \sin P)][s (\cos Q + i \sin Q)] = rs[\cos(P+Q)+i\sin(P+Q)] \end{equation*}

In words, multiplying complex numbers involves multiplying their distances from the origin, and adding their angles.

We can derive a similar formula for dividing complex numbers. That formula is

\begin{equation*} \frac{r (\cos P + i \sin P)}{s (\cos Q + i \sin Q)} = \frac{r}{s}[\cos(P-Q)+i\sin(P-Q)] \end{equation*}

Powers and roots

Since exponents represent repeated multiplication, we can derive a formula for powers of complex numbers. That formula is known as DeMoivre's Theorem:

\begin{equation*} \left[r(\cos P+i\sin P) \right]^n = r^n (\cos nP + i \sin nP) \end{equation*}

We can also use this formula to do roots, by using fractions for the variable $n$. However, roots are not unique, since the trigonometric functions are periodic. The formula which gives the $n$th roots is

\begin{equation*} [r (\cos P + i \sin P)]^{\frac{1}{n}} = r^\frac{1}{n} \left( \cos \frac{P+2k\pi}{n}+i\sin \frac{P+2k\pi}{n} \right) \end{equation*}

Notice that this formula not only does square roots, but all kinds of roots.

So what is the square root of $2+3i$? In trigonometric form, the original number is $\sqrt{13}(\cos P + i\sin P)$, where the angle $P = \arctan \frac32$. Therefore, the square roots are $\sqrt{\sqrt{13}}\left( \cos\frac12\arctan\frac32+i\sin\frac12\arctan\frac32\right)$ and $\sqrt{\sqrt{13}}\left( \cos(\pi+\frac12\arctan\frac32)+i\sin(\pi+\frac12\arctan\frac32)\right)$.

Epilogue

Of course, now we can simply ask some hand held calculators to do our complex number arithmetic. Unfortunately, the calculator doesn't tell us why the answers are the way they are. This discussion was intended to help our understanding.

Now, if you have mastered square roots of imaginary numbers, are you ready for imaginary numbers as exponents? If so, read Using i as an Exponent.

Back to introduction.