Arithmetic Sequences

Given a sequence described by a list of numbers, often having a formula for the sequence will be useful. Keep in mind, though, that many different formulas are possible for the same few initial terms of the list. However, certain patterns result in simpler formulas than other patterns, and it is these simple patterns that we generally seek.

Common Differences and Arithmetic Sequences

Consider the sequence $14, 17, 20, 23, 26, 29, 32, \ldots$ Upon inspection, we might notice that consecutive terms are always the same distance from one another. This can be seen more clearly if we write the differences in a row underneath the spaces between the terms, as in the following diagram

\begin{equation*} \begin{array}{ccccccccc} 14, & \phantom. & 17, & \phantom. & 20, & \phantom. & 23, & \phantom. & 26,\ldots \\ \phantom. & +3 & \phantom. & +3 & \phantom. & +3 & \phantom. & +3 & \phantom. \end{array} \end{equation*}

Whenever the consecutive terms of a sequence differ by a constant, the sequence is called an arithmetic sequence. The difference between consecutive terms is called the common difference, and is often identified by the variable $d$.

In our specific example, the common difference $d=3$. This pattern immediately implies that the recursive formula is $a_n=a_{n-1}+3,\quad a_1=14$. Furthermore, we see that the second term was produced by adding three once, the third term was produced by adding three twice, and in general the $n$th term is produced by adding three a total of $n-1$ times. Therefore, the explicit formula is $a_n=14+3(n-1)$, or after simplifying, $a_n=3n+11$.

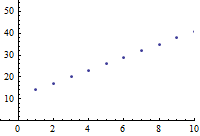
graph of a sub n equals a sub n minus 1 plus 3, a sub 1 equals 14

In general, the recursive formula of an arithmetic sequence always has the form $a_n=a_{n-1}+d$, and the explicit formula always has the form $a_n=a_1+d(n-1)$. In particular, the explicit formula of an arithmetic sequence will always be linear, as is illustrated in the graph of this arithmetic sequence above.

The arithmetic sequence is used in a variety of applications. Examples include:

The seats in an auditorium are arranged in a semicircular pattern. The first row has 24 seats, and each succeeding row has an additional 2 seats. This is an arithmetic sequence with first term 24 and common difference 2.
Campbell County's grain production was 150 million bushels in 1990, and since then has been increasing by 3 million bushels per year. This is an arithmetic sequence with first term 150 million and common difference 3 million.

Epilogue

Common differences are one of the two easiest situations. Another very common situation in a sequence is to have a common ratio. See the page Geometric Sequences for more information.