
We use MathJax
Averages cannot tell the entire story of a data set. Consider, for example, the following three data sets, giving the heights of the starters of three high school basketball teams.
| Bulls | $\qquad 70", 71", 72", 73", 74"$ |
| Eagles | $\qquad 66", 71", 72", 73", 78"$ |
| Pythons | $\qquad 66", 67", 72", 77", 78"$ |
Each of these data sets has a mean of 72 inches, a median of 72 inches, and no mode. But the heights of the players on these teams are not identical. The players on the Bulls are quite alike in height, but the heights of the other teams are more spread out. We would like to measure the spread, or dispersion, of the heights.
The most obvious way to measure spread would be to calculate the difference between the extreme values of the set. This is called the range, and it is found by subtracting the minimum from the maximum. For the Bulls, the range is 4 inches, and for the Eagles and Pythons the range is 12 inches. So we see the range did distinguish one of the three teams, but not the other two.
Caution: The range used in statistics is not the same as the range of a function from algebra and calculus. The range of a function is an interval of $y$-values, and a possible answer might be $[66,78]$. But the range in statistics is a single value equal to the difference of these, that is, 12 inches. In statistics, we always want the single-valued range.
The range did not distinguish between all three teams because it only took into account two of the values on each team, and ignored all of the rest of the values. If we want to consider all of the values, we need a quantity that will use all of them in the computation. To do that, we first consider the deviation, or difference from the mean. Symbolically, the deviation is the quantity $x_i - \bar{x}$ , if sample data is being used, or $x_i-\mu$, if population data is being used. Here are the deviations for the three teams.
| Bulls | $\qquad -2", -1", 0", 1", 2"$ |
| Eagles | $\qquad -6", -1", 0", 1", 6"$ |
| Pythons | $\qquad -6", -5", 0", 5", 6"$ |
To obtain a single number, we might decide to find an average of the deviations. But if we compute either the mean or the median of these numbers, we will always obtain zero. And just as the original data, the deviations also have no mode. We undoubtedly recognize that the presence of the negative signs is what has caused this result.
What if we ignore the negative signs? Or more mathematically, take absolute values? We can then obtain a quantity called the mean absolute deviation. The formula for this quantity is $\dfrac{\sum\limits_{i=1}^n |x_i-\bar{x}|}{n}$, if sample data is used, with a similar formula for population data. Computing the mean absolute deviation of the starter heights for each team, we get 1.2 inches for the Bulls, 2.8 inches for the Eagles, and 4.4 inches for the Pythons. The mean absolute deviation does distinguish between the three data sets.
However, in the formula of the mean absolute deviation their lurks a difficulty. It uses absolute values. When dealing with absolute values in former math classes, what did you usually have to do? Probably you had to break the problem into cases. That is not a direction we really want to go, so we will set aside this formula.
Another approach to removing the negative signs is to square each of the quantities. This approach yields two measures of dispersion, one called the variance, and its square root that is called the standard deviation. The formulas are as follows:
| Population Formula | Sample Formula | |
| Variance | $\sigma^2=\dfrac{\sum\limits_{i=1}^N (x_i-\mu)^2}{N}$ | $s^2=\dfrac{\sum\limits_{i=1}^n (x_i-\bar{x})^2}{n-1}$ |
| Standard Deviation | $\sigma=\sqrt{\dfrac{\sum\limits_{i=1}^N (x_i-\mu)^2}{N}}$ | $s=\sqrt{\dfrac{\sum\limits_{i=1}^n (x_i-\bar{x})^2}{n-1}}$ |
Besides the use of sample or population formulas for the mean and the size of the data set, there is another very important difference. The sample formulas have a different denominator. That is because the sample formula is intended to be used as an estimator for the population parameter, and to obtain an unbiased estimator (one that will not be too small on the average) it is necessary to use the smaller denominator.
Let us compute the variance and standard deviation of the heights for the population of the starters on the Eagles. The computation is:
$\sigma^2=\dfrac{\sum\limits_{i=1}^N (x_i-\mu)^2}{N}
=\dfrac{(66"-72")^2+(71"-72")^2+(72"-72")^2+(73"-72")^2+(78"-72")^2}{5}$
$\qquad =\dfrac{((-6)^2+(-1)^2+0^2+1^2+6^2) \text{ square inches}}{5}
=\dfrac{(36+1+0+1+36) \text{ square inches}}{5}$
$\qquad =\dfrac{74}{5}\text{ square inches}=14.8 \text{ square inches}$
$\sigma = \sqrt{\dfrac{74}{5}\text{ square inches}} = \dfrac{\sqrt{370}}{5}\text{ inches}
\approx 3.85 \text{ inches}$
So the population variance for the Eagles is 14.8 square inches, and the population standard deviation for the Eagles is approximately 3.85 inches. If we had used the sample formulas, we would have obtained a variance of 18.5 inches, and a standard deviation of approximately 4.30 inches.
Having kept track of the units, we can see why the square root proved necessary. We were attempting to find a way to measure average distance, so we needed a result whose units would be distance. Variance produced a unit of area, not of distance. Even though the units are different, variance does occur often enough in a study of statistics to warrant its own name.
When computing the standard deviation from a frequency distribution, a weighted formula is required. The formulas are as follows:
| Population Formula | Sample Formula | |
| Variance | $\sigma^2=\dfrac{\sum\limits_{i=1}^N w_i (x_i-\mu)^2}{\sum\limits_{i=1}^N w_i}$ | $s^2=\dfrac{\sum\limits_{i=1}^n w_i(x_i-\bar{x})^2}{\left(\sum\limits_{i=1}^n w_i\right)-1}$ |
| Standard Deviation | $\sigma=\sqrt{\dfrac{\sum\limits_{i=1}^N w_i(x_i-\mu)^2}{\sum\limits_{i=1}^N w_i}}$ | $s=\sqrt{\dfrac{\sum\limits_{i=1}^n w_i(x_i-\bar{x})^2} {\left(\sum\limits_{i=1}^n w_i\right)-1}}$ |
Suppose the heights of 169 freshmen at Western High School were found, and the results provided in the following table.
| Height | Number of Students |
| 135-149 cm | 23 |
| 150-164 cm | 36 |
| 165-179 cm | 29 |
| 180-194 cm | 64 |
| 195-209 cm | 17 |
This is the same example that we used on the page Measures of Central Tendency. There, we found the mean $\bar{x} =\frac{29308}{169} \approx 173.42$ cm. Now we compute the standard deviation, showing the details in the following table:
| Height | Class Midpoints $x_i$ |
Deviations $x_i - \bar{x}$ | Number of Students $w_i$ |
Weighted Squared Deviations $w_i (x_i - \bar{x})^2$ |
| 135-149 cm | 142 cm | $-31.42$ cm | 23 | 22705.98 cm2 |
| 150-164 cm | 157 cm | $-16.42$ cm | 36 | 9706.19 cm2 |
| 165-179 cm | 172 cm | $-1.42$ cm | 29 | 58.48 cm2 |
| 180-194 cm | 187 cm | $13.58$ cm | 64 | 11802.65 cm2 |
| 195-209 cm | 202 cm | $28.58$ cm | 17 | 13885.88 cm2 |
| Totals | 169 | 58159.18 cm2 |
We then have $s^2=\dfrac{58159.18}{169} \approx 344.14$ cm2, which gives $s \approx \sqrt{344.14} \approx 18.55$ cm.
The standard deviation certainly tells us something about an average distance data values fall from the mean. But an average also places restrictions on where data can fall. The following theorem quantifies that restriction.
Chebyshev's Theorem: For any distribution of data having a finite mean and a finite standard deviation, at least $1-\dfrac{1}{z^2}$ of the data will fall within $z$ standard deviations of the mean.
Let us test this result on the starter heights of the Eagles, using 2 standard deviations. We had earlier found that the Eagles had a mean height of 72 inches, and a standard deviation of approximately 3.85 inches. There are three stages to the verification.
Chebyshev's Theorem is always true for any data set, and it places a restriction on how spread out the data will be. On the other hand, the formula does not provide any useful information for $z\le 1$, since it will tell us that at least 0% of the data will fall within that interval. But this is to be expected from a formula that works for every possible data set. There can be a lot of variety, and Chebyshev's Theorem must accommodate all of that variety. If we restrict the variety possible, we can obtain a more specific result. For a proof, see Expected Value and Variance Properties.
Empirical Rule: If a data set is approximately normally distributed (bell-shaped), then
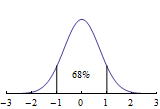
A justification for this result can be found in Normal Distributions.
A great many physical phenomena that allow variation will be approximately normally distributed, so this is a very useful result. When testing a given data set, all three statements of the Empirical Rule must be found reasonable to conclude that the Empirical Rule is satisfied. Doing this for the starter heights of the Eagles, we find
The percentages obtained from the starter heights of the Eagles are somewhat close, but not really close. Based on those results, we should have doubts about whether the Empirical Rule applies. Graphing the data would suggest that we do have something similar to a bell-shaped curve, but not near as smooth a curve.
Standard deviations are measured in the same unit as the data, since the conceptual idea is an average "distance" from the mean. But if you want to compare the spreads of two very different data sets, you need to have units which are identical. This can be done with the coefficient of variation, given by the formula $\dfrac{\sigma}{\mu}\times 100\%$, or the equivalent formula using sample data. The coefficient of variation is a ratio, and therefore unitless.
For example, suppose we know that teacher salaries in a local school district have $\mu=\$58,000$ and $\sigma=\$6,000$. We also know that a sample of human birth weights finds $\bar{x}=114\text{ ounces}$ and $s=21\text{ ounces}$. Computing the coefficients of variation, we find a ratio of $\dfrac{6000}{58000}\times 100\%=10.34\%$ for the teacher salaries, and $\dfrac{21}{114}\times 100\%=18.42\%$ for birth weights. In this case, the birth weights of humans show more spread than the salaries of the teachers.