
We use MathJax
The equation of each curve is a third-degree polynomial function of two variables, and can be written in the form $a_1x^3+a_2x^2y+a_3xy^2+a_4y^3+a_5x^2+a_6xy+a_7y^2+a_8x+a_9y+a_{10}=0$. One property common to each of these curves is that it will intersect any given line at most 3 times.
Each of the graphs on this page is a cubic plane curve, displayed in the window $[-5,5]\times[-5,5]$.
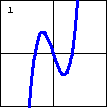 |
$x^3-3x-y=0$ Here is a typical cubic polynomial function. The range of a cubic function is all real numbers. The bend in the graph can be more or less pronounced. Rotating this shape can give another cubic plane curve, but then it may not be a function. |
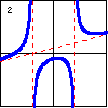 |
$x^3-x^2y+2x^2-4x+4y+8=0$ A cubic plane curve can have 3 linear asymptotes. Here, two of the asymptotes are parallel. |
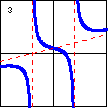 |
$x^3-x^2y+2x^2+4x+4y-8=0$ Here is another cubic plane curve with three linear asymptotes, where two are parallel. But this time, the graph crosses one of the asymptotes. |
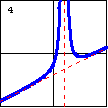 |
$x^3-2x^2y-6x^2+4xy+9x-2y-2=0$ This cubic plane curve has just two linear asymptotes. Actually, one of the asymptotes has multiplicity two. |
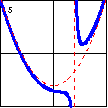 |
$x^3-2x^2-3xy-9x+6y+21=0$ Here is a cubic plane curve which has one linear and one parabolic asymptote. In this graph, the linear asymptote is parallel to the axis of symmetry of the parabola. Newton's Trident has a similar, but slightly easier, equation. |
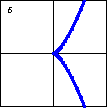 |
$x^3-y^2=0$ This graph is often called a semicubical parabola. The sharp corner point at the origin is called a cusp. The two branches both have zero slope at the cusp. |
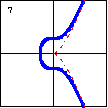 |
$x^3-y^2+2=0$ This cubic plane curve is asymptotic to the semicubical parabola. |
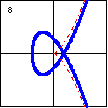 |
$x^3-y^2-3x+2=0$ Here is another cubic plane curve which is asymptotic to the semicubical parabola. The intersection point where the graph crosses itself is called a node. |
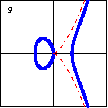 |
$x^3-y^2-3x=0$ Here is another cubic plane curve which is asymptotic to the semicubical parabola. It also has a closed branch, called a conjugate oval. |
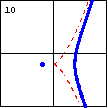 |
$x^3-y^2-3x-2y-3=0$ This cubic plane curve is also asymptotic to the semicubical parabola, but its conjugate oval has degenerated into a single point. |
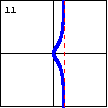 |
$xy^2-y^2+x=0$ A cubic curve can be asymptotic to a line. The Witch of Agnesi is this type of curve. |
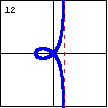 |
$3x^3+5xy^2+5x^2-5y^2=0$ This cubic curve is asymptotic to a line, and crosses itself at a node located at the origin. The Trisectrix of Maclaurin is this type of curve. The Folium of Descartes is also this type of curve, but with a diagonal asymptote. |
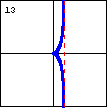 |
$x^3+xy^2-y^2=0$ This cubic curve is asymptotic to a line, and has a cusp at the origin. |
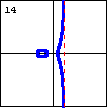 |
$3x^3+5xy^2+5x^2-5y^2-1=0$ Here is a cubic curve that is asymptotic to a line, and has a conjugate oval. |
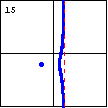 |
$729x^3+1215xy^2+1215x^2+2430xy-1215y^2+1215x-2430y-1715=0$ A cubic curve can also have an isolated point and be asymptotic to a line. |
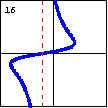 |
$xy^2+y^2+x-6y+1=0$ Here is a cubic curve that is asymptotic to a line, but also crosses that asymptote. |
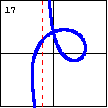 |
$x^3+xy^2-2x^2+y^2-4x-4y+4=0$ A cubic curve can cross both itself and its asymptote. |
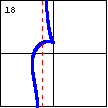 |
$x^3+xy^2+x^2+y^2-x-2y+1=0$ This cubic curve crosses its asymptote, and has a cusp. |
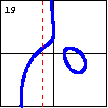 |
$x^3+xy^2-2x^2+4xy+y^2-3x-4y+4=0$ This cubic curve crosses its asymptote, and has a second closed branch. |
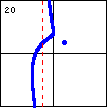 |
$x^3+xy^2-x^2+y^2-2x-4y+4=0$ This curve is similar to the previous curve, except that the oval has shrunk into an isolated point. |
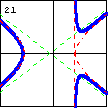 |
$3x^3-5xy^2-4x^2+10y^2-21x+42=0$ This is the first of several cubic curves with three linear asymptotes. A small change in the constant will not produce three lines, but instead will produce a line and a hyperbola. |
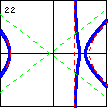 |
$3x^3-5xy^2-4x^2+10y^2-45x+90=0$ Here is another variety whose degenerate case is a line and a hyperbola. |
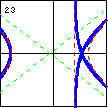 |
$9x^3-15xy^2-12x^2+30y^2-128x+256=0$ Here, we have a cubic curve with a node where two branches cross, and a degenerate case of a line and a hyperbola. |
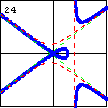 |
$3x^3-5xy^2-4x^2+10y^2=0$ A cubic curve can also have a node where one branch crosses itself, while having a degenerate case of a line and a hyperbola. |
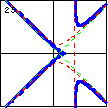 |
$x^3-xy^2-3x^2+2y^2+3x-1=0$ Here, we have a cubic curve with a cusp, and a degenerate case of a line and a hyperbola. |
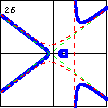 |
$6x^3-10xy^2-8x^2+20y^2-x+2=0$ Here we have a conjugate oval, as well as a degenerate case of a line and a hyperbola. |
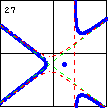 |
$3x^3-5xy^2-4x^2-10xy+10y^2-6x+20y+12=0$ Here we have an isolated point, as well as a degenerate case of a line and a hyperbola. |
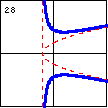 |
$xy^2-x^2+y^2-2x-5=0$ This is the first of several cubic curves having a line and a parabola for asymptotes. |
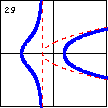 |
$xy^2-x^2+y^2-2x+3=0$ Here is another cubic curve with a line and a parabola with asymptotes. |
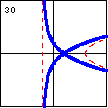 |
$xy^2-x^2+y^2+2x-1=0$ A cubic curve with linear and parabolic asymptotes can also have a node where its two branches cross. |
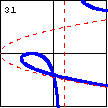 |
$xy^2-x^2-y^2-4x-4y-4=0$ A cubic curve with linear and parabolic asymptotes can also have a node where one branch crosses itself. |
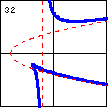 |
$xy^2-x^2+y^2-5x-2y-7=0$ A cubic curve with linear and parabolic asymptotes can also have a cusp. |
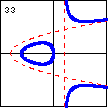 |
$xy^2-x^2-y^2-3x=0$ A cubic curve with linear and parabolic asymptotes can also have a conjugate oval. |
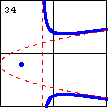 |
$xy^2-x^2+y^2-6x-9=0$ A cubic curve with linear and parabolic asymptotes can also have an isolated point. |
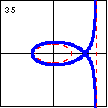 |
$x^3+4xy^2-4x^2-16y^2-3x+18=0$ Here is another cubic curve with a node. If the constant were changed appropriately, this curve would degenerate into a line and an ellipse. |
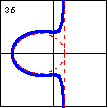 |
$3x^3+5xy^2+5x^2-5y^2-20x+20=0$ Here is another cubic curve whose degenerate case is a line and an ellipse. |
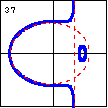 |
$3x^3+5xy^2-4x^2-10y^2-45x+90=0$ A cubic curve can have branches both inside and outside of its degenerate ellipse. |
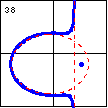 |
$9x^3+15xy^2-12x^2+30xy-30y^2-113x-60y+226=0$ A cubic curve can have an isolated point inside its degenerate ellipse. |
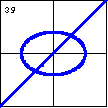 |
$4x^3-4x^2y+9xy^2-9y^3-36x+36y=0$ An ellipse and a line is one of the degenerate cases of a cubic curve. |
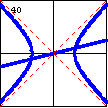 |
$x^3-4x^2y-xy^2+4y^3-4x+16y=0$ A hyperbola and a line is also a degenerate cubic curve. |
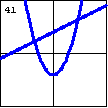 |
$x^3-2x^2y+4x^2-xy+2y^2-2x-8=0$ A parabola and a line can be a degenerate cubic curve. |
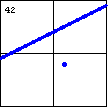 |
$x^3-2x^2y+xy^2-2y^3-6x^2+6xy-8y^2+10x-12y-8=0$ A line and an isolated point is another type of degenerate cubic curve. |
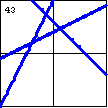 |
$2x^3-3x^2y-3xy^2+2y^3+7x^2+14xy-20y^2-19x+62y-60=0$ Three lines (which could be intersecting or parallel) is another case of a degenerate cubic plane curve. |
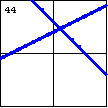 |
$x^3-3xy^2-2y^3-2x^2+14xy+16y^2-15x-42y+36=0$ If one of the lines is doubled (with a factor that is squared), then the graph of a cubic equation can be two lines. |
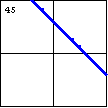 |
$x^3+3x^2y+3xy^2+y^3-9x^2-18xy-9y^2+27x+27y-27=0$ If a line is tripled (with a factor that is cubed), or if a curve has an "imaginary ellipse" as a factor, then the graph of a cubic equation can be a single line. |